题目内容
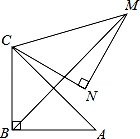
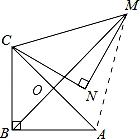
如图,在Rt△ABC中,∠ABC=90°,AB=BC=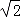 ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
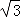 +1 .
+1 .
【考点】旋转的性质;全等三角形的判定与性质;角平分线的性质;等边三角形的判定与性质;等腰直角三角形.
【专题】压轴题.
【分析】如图,连接AM,由题意得:CA=CM,∠ACM=60°,得到△ACM为等边三角形根据AB=BC,CM=AM,得出BM垂直平分AC,于是求出BO=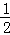 AC=1,OM=CM•sin60°=
AC=1,OM=CM•sin60°=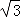 ,最终得到答案BM=BO+OM=1+
,最终得到答案BM=BO+OM=1+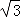 .
.
【解答】解:如图,连接AM,
由题意得:CA=CM,∠ACM=60°,
∴△ACM为等边三角形,
∴AM=CM,∠MAC=∠MCA=∠AMC=60°;
∵∠ABC=90°,AB=BC= ,
,
∴AC=2=CM=2,
∵AB=BC,CM=AM,
∴BM垂直平分AC,
∴BO=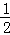 AC=1,OM=CM•sin60°=
AC=1,OM=CM•sin60°=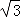 ,
,
∴BM=BO+OM=1+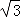 ,
,
故答案为:1+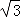 .
.
【点评】本题考查了图形的变换﹣旋转,等腰直角三角形的性质,等边三角形的判定和性质,线段的垂直平分线的性质,准确把握旋转的性质是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 与x轴交于点A(
与x轴交于点A( ,0)、B(4,0)两点,与y轴交于点C.
,0)、B(4,0)两点,与y轴交于点C.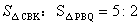 ,求K点坐标.
,求K点坐标.

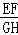 的值是( )
的值是( )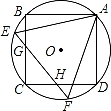
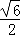 B.
B.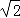 C.
C.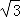 D.2
D.2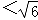 时,请直接写出x1和x2的取值范围.
时,请直接写出x1和x2的取值范围. )×(
)×( -
-  );
);