题目内容
已知关于x的方程(x﹣3)(x﹣2)﹣p2=0.
(1)求证:方程总有两个不相等的实数根.
(2)设方程的两根为x1,x2(x1<x2),则当0≤p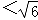 时,请直接写出x1和x2的取值范围.
时,请直接写出x1和x2的取值范围.
【考点】根的判别式;根与系数的关系.
【专题】计算题;一次方程(组)及应用.
【分析】(1)方程整理为一般形式,表示出根的判别式,根据根的判别式的值为正数,即可得证;
(2)根据p的范围,表示出两根的取值范围即可.
【解答】(1)证明:方程可变形为x2﹣5x+6﹣p2=0,
∵△=25﹣4(6﹣p2)=4p2+1>0,
∴方程总有两个不相等的实数根;
(2)解:设方程的两根为x1,x2(x1<x2),
则当0≤p 时,x1和x2的取值范围分别为0<x1≤2,3≤x2<5.
时,x1和x2的取值范围分别为0<x1≤2,3≤x2<5.
【点评】此题考查了根的判别式,以及根与系数的关系,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 x﹣4)=1﹣2x;
x﹣4)=1﹣2x;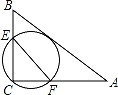
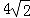 B.4.75 C.5 D.4.8
B.4.75 C.5 D.4.8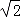 ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .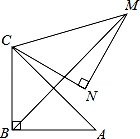

 -1=
-1= .
.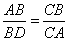 D.
D.