题目内容
如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( )

A.80° B.100° C.110° D.130°
D【考点】圆周角定理.
【分析】连接OC,然后根据等边对等角可得:∠OCB=∠OBC=40°,然后根据三角形内角和定理可得∠BOC=100°,然后根据周角的定义可求:∠1=260°,然后根据圆周角定理即可求出∠A的度数.
【解答】解:连接OC,如图所示,

∵OB=OC,
∴∠OCB=∠OBC=40°,
∴∠BOC=100°,
∵∠1+∠BOC=360°,
∴∠1=260°,
∵∠A=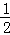 ∠1,
∠1,
∴∠A=130°.
故选:D.
【点评】此题考查了圆周角定理.此题比较简单,注意掌握数形结合思想的应用,解题的关键是:熟记在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 .
. x﹣4)=1﹣2x;
x﹣4)=1﹣2x;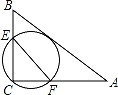
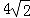 B.4.75 C.5 D.4.8
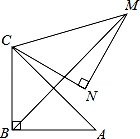
B.4.75 C.5 D.4.8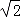 ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .