题目内容
10．
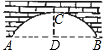如图，圆弧形桥拱的跨度AB=24米，拱高CD=8米，则拱桥的半径为（ ）| A． | 6.5米 | B． | 9米 | C． | 13米 | D． | 15米 |
分析 根据垂径定理的推论，知此圆的圆心在CD所在的直线上，设圆心是O．连接OA．根据垂径定理和勾股定理求解．
解答 
解：根据垂径定理的推论，知此圆的圆心在CD所在的直线上，设圆心是O
连接OA．根据垂径定理，得AD=12m，
设圆的半径是r，根据勾股定理，
得r2=122+（r-8）2，
解得r=13．
故选：C．
点评 此题主要考查了勾股定理以及垂径定理的应用．注意构造由半径、半弦、弦心距组成的直角三角形进行有关的计算．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．不等式组$\left\{\begin{array}{l}{2x-1＞1}\\{4-2x≤0}\end{array}\right.$的解集是（ ）
| A． | x≤2 | B． | 1＜x≤2 | C． | x＞1 | D． | x≥2 |
2．下列变形正确的是（ ）
| A． | $\frac{-x}{x-y}=\frac{x}{x+y}$ | B． | $\frac{y}{x}=\frac{{y}^{2}}{{x}^{2}}$ | C． | $\frac{x}{y}=\frac{ax}{ay}$ | D． | $\frac{m}{n}=\frac{m（{x}^{2}+1）}{n（{x}^{2}+1）}$ |
