Question

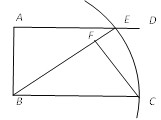
【题目】如图，点A在线段BD上，在BD的同侧作等腰Rt△ABC和等腰Rt△ADE，CD与BE、AE分别交于点P，M．对于下列结论：①△BAE∽△CAD；②MPMD＝MAME；③2CB2＝CPCM．其中正确的是（　 　）

A. ①②③ B. ① C. ①② D. ②③

Answer 1

【答案】A

【解析】

①根据等腰三角形的性质，得到，即，根据对应边成比例，得到△BAE∽△CAD；

②由①中△BAE∽△CAD，得，证明△PME∽△AMD，得到，即MPMD＝MAME，

③由②中△PME∽△AMD，得，由，得证△PMA∽△EMD，再证明△APC∽△MAC，得到，即，因为，所以.

①在等腰和等腰中，

，，，

所以，即，

又因为，

所以△BAE∽△CAD，

故①正确；

②由①中△BAE∽△CAD，得，

又因为，

所以△PME∽△AMD，

所以，即MPMD＝MAME，

故②正确.

③由②中△PME∽△AMD，得，

因为MPMD＝MAME，

所以，所以△PMA∽△EMD，

所以，

因为，，

所以△APC∽△MAC，

所以，即，

又因为，

所以，

故③正确.所以答案选A.