题目内容
5. 如图,在△ABC中,AC边的垂直平分线DM交AC于D,BC边的垂直平分线EN交BC于E,DM与EN相交于点F
如图,在△ABC中,AC边的垂直平分线DM交AC于D,BC边的垂直平分线EN交BC于E,DM与EN相交于点F(1)若△CMN的周长为20cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
分析 (1)根据线段的垂直平分线的性质得到MA=MC,NB=NC,根据三角形的周长公式计算即可;
(2)根据四边形内角和定理和等腰三角形的性质求出∠A+∠B=70°,由∠MCA=∠A,∠NCB=∠B,计算即可.
解答 解:(1)∵DM是AC边的垂直平分线,
∴MA=MC,
∵EN是BC边的垂直平分线,
∴NB=NC,
AB=AM+MN+NB=MC+MN+NC=△CMN的周长=20cm;
(2)∵MD⊥AC,NE⊥BC,
∴∠ACB=180°-∠MFN=110°,
∴∠A+∠B=70°,
∵MA=MC,NB=NC,
∴∠MCA=∠A,∠NCB=∠B,
∴∠MCN=40°.
点评 本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键,注意三角形内角和定理的应用.

练习册系列答案
相关题目
13.在-2,3,4,-5这四个数中,任取两个数相乘,所得积最小的是( )
| A. | -8 | B. | -20 | C. | -6 | D. | 10 |
20.由下列条件不能判定△ABC为直角三角形的是( )
| A. | ∠A+∠C=∠B | B. | a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$ | C. | (b+a)(b-a)=c2 | D. | ∠A:∠B:∠C=5:3:2 |
17.抛物线y=$\frac{1}{2}$x2的顶点坐标是( )
| A. | ($\frac{1}{2}$,0) | B. | (0,0) | C. | (0,-$\frac{1}{2}$) | D. | (-$\frac{1}{2}$,0) |
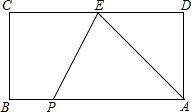 如图,长方形ABCD,AB=18,AD=8,E为CD边上一点,CE=12,
如图,长方形ABCD,AB=18,AD=8,E为CD边上一点,CE=12,