Question

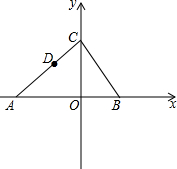如图，点A、B的坐标分别是（-5，0），（3，0），C的坐标为（0，4），点D在线段AC上，且S_△AOD=

5

16

S_△ABC
（1）求△ABC的面积；
（2）求D的坐标．

Answer 1

考点：坐标与图形性质,三角形的面积

专题：计算题

分析：（1）直接根据三角形面积公式计算；
（2）先利用待定系数法求出直线AC的解析式为y=

4

5

x+4，设设D（t，

4

5

t+4），则利用S_△AOD=

5

16

S_△ABC得到

1

2

×4×（

4

5

t+4）=

5

16

×16，然后解方程求出t即可得到D点坐标．

解答：解：（1）∵A（-5，0），B（3，0），C（0，4），
∴△ABC的面积=

1

2

×（3+5）×4=16；
（2）设直线AC的解析式为y=kx+b，
把A（-5，0），C（0，4）分别代入得

-5k+b=0 b=4

，解得

k= 4 5 b=4

，
∴直线AC的解析式为y=

4

5

x+4，
设D（t，

4

5

t+4），
∵S_△AOD=

5

16

S_△ABC，
∴

1

2

×4×（

4

5

t+4）=

5

16

×16，解得t=-

15

8

，
∵D点坐标为（-

15

8

，

5

2

）．

点评：本题考查了坐标与图形性质：利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系；记住特殊位置点的坐标特征．也考查了三角形的面积公式．