题目内容
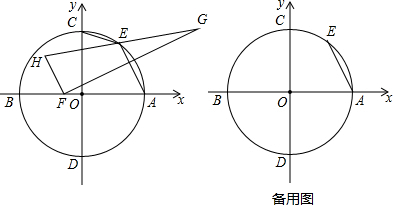
5.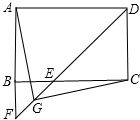 如图,在矩形ABCD中,∠ADC的平分线交BC于点E、交AB的延长线于点F,G是EF的中点,连接AG、CG.
如图,在矩形ABCD中,∠ADC的平分线交BC于点E、交AB的延长线于点F,G是EF的中点,连接AG、CG.(1)求证:BE=BF;
(2)请判断△AGC的形状,并说明理由.
分析 (1)由矩形的性质结合角平分线的定义可证得∠ADF=∠BEF=∠CDF=∠F,可证明BE=BF;
(2)连接BG,可证明△AGF≌△CGB,可证得AG=CG,进一步可证明∠AGC=90°,可判定△AGC为等腰直角三角形.
解答 (1)证明:∵四边形ABCD为矩形,
∴AB∥CD,AD∥BC,
∴∠F=∠CDF,∠ADF=∠BEF,
∵DF平分∠ADC,
∴∠CDF=∠ADF,
∴∠F=∠BEF,
∴BE=BF;
(2)解:△AGC为等腰直角三角形,理由如下:
如图,连接BG,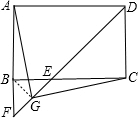
由(1)可知BE=BF,且∠FBE=90°,
∴∠F=45°,
∴AF=AD=BC,
∵G为EF中点,
∴BG=FG,∠EBG=45°,
在△AGF和△CGB中,
$\left\{\begin{array}{l}{GF=GB}\\{∠F=∠CBG}\\{AF=BC}\end{array}\right.$,
∴△AGF≌△CGB(SAS),
∴AG=CG,∠AGF=∠BGC,
∴∠BGF+∠AGB=∠AGB+∠AGC,
∴∠AGC=∠BGF=90°,
∴△AGC为等腰直角三角形.
点评 本题主要考查全等三角形的判定和性质和矩形的性质,在(1)中充分利用矩形的对边分别平行是解题的关键,在(2)构造三角形全等是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
13.在函数y=$\frac{1}{\sqrt{x+3}}$中,自变量x的取值范围是( )
| A. | x<-3 | B. | x≥3 | C. | x≤-3 | D. | x>-3 |
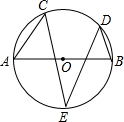 如图,AB是⊙O的直径,C、D、E都是⊙O上的点,∠A=55°,∠B=70°,则∠E的度数是35°.
如图,AB是⊙O的直径,C、D、E都是⊙O上的点,∠A=55°,∠B=70°,则∠E的度数是35°.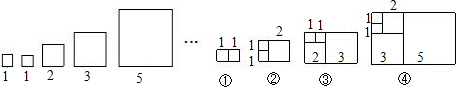
 用含字母a的算式表示图中阴影部分的面积.
用含字母a的算式表示图中阴影部分的面积.