题目内容
15.(1)计算:$\root{3}{-8}$-(-$\frac{1}{2}$)-1-|$\sqrt{3}$-2|-tan60°(2)先化简,再求值:($\frac{a}{ab-{b}^{2}}$-$\frac{b}{ab-{a}^{2}}$)÷$\frac{{a}^{2}+{b}^{2}}{ab}$,已知a=$\sqrt{5}$+2,b=$\sqrt{5}$-2.
分析 (1)原式第一项利用立方根定义计算,第二项利用负整数指数幂法则计算,第三项利用绝对值的代数意义化简,最后一项利用特殊角的三角函数值计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a与b的值代入计算即可求出值.
解答 解:(1)原式=-2-(-2)-2+$\sqrt{3}$-$\sqrt{3}$=-2;
(2)原式=[$\frac{a}{b(a-b)}$-$\frac{b}{a(b-a)}$]•$\frac{ab}{{a}^{2}+{b}^{2}}$=$\frac{{a}^{2}+{b}^{2}}{ab(a-b)}$•$\frac{ab}{{a}^{2}+{b}^{2}}$=$\frac{1}{a-b}$,
当a=$\sqrt{5}$+2,b=$\sqrt{5}$-2时,原式=1.
点评 此题考查了实数的运算,以及分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
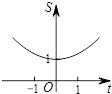
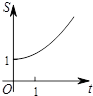
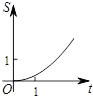
 如图,在平面直角坐标系中,点C的坐标为(0,2),动点A以每秒1个单位长的速度从点O出发沿x轴的正方向运动,M是线段AC的中点,将线段AM以点A为中心,沿顺时针方向旋转90°得到线段AB.联结CB.设△ABC的面积为S,运动时间为t秒,则下列图象中,能表示S与t的函数关系的图象大致是( )
如图,在平面直角坐标系中,点C的坐标为(0,2),动点A以每秒1个单位长的速度从点O出发沿x轴的正方向运动,M是线段AC的中点,将线段AM以点A为中心,沿顺时针方向旋转90°得到线段AB.联结CB.设△ABC的面积为S,运动时间为t秒,则下列图象中,能表示S与t的函数关系的图象大致是( )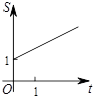
 如图,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.
如图,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.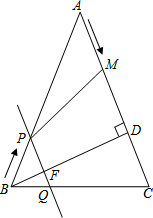 已知如图,在△ABC中,AB=AC=10$\sqrt{2}$cm,∠BAC=45°,BD⊥AC于D,点M从点A出发,沿AC方向匀速运动,速度为2cm/s,同时直线PQ由点B出发沿BA方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于P,交BC于Q,交BD于F,连接PM,设运动时间为t(s)(0<t<5$\sqrt{2}$),解答下列问题:
已知如图,在△ABC中,AB=AC=10$\sqrt{2}$cm,∠BAC=45°,BD⊥AC于D,点M从点A出发,沿AC方向匀速运动,速度为2cm/s,同时直线PQ由点B出发沿BA方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于P,交BC于Q,交BD于F,连接PM,设运动时间为t(s)(0<t<5$\sqrt{2}$),解答下列问题: 如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=8,PB=4,则cosP的值为$\frac{4}{5}$.
如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=8,PB=4,则cosP的值为$\frac{4}{5}$.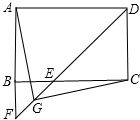 如图,在矩形ABCD中,∠ADC的平分线交BC于点E、交AB的延长线于点F,G是EF的中点,连接AG、CG.
如图,在矩形ABCD中,∠ADC的平分线交BC于点E、交AB的延长线于点F,G是EF的中点,连接AG、CG.