题目内容
二次函数的图象经过点A(0,-3),B(2,-3),C(-1,0).
(1)求此二次函数的关系式;
(2)求此二次函数图象的顶点坐标.
(1)求此二次函数的关系式;
(2)求此二次函数图象的顶点坐标.
考点:待定系数法求二次函数解析式,二次函数的性质
专题:计算题
分析:(1)设一般式y=ax2+bx+c,再把三个点的坐标分别代入得到关于a、b、c的方程组,然后解方程组求出a、b、c的值,从而得到二次函数解析式;
(2)先把(1)中的解析式配成顶点式,然后根据二次函数的性质确定顶点坐标.
(2)先把(1)中的解析式配成顶点式,然后根据二次函数的性质确定顶点坐标.
解答:解:(1)设二次函数解析式为y=ax2+bx+c,
根据题意得
,解得
,
所以二次函数解析式为y=x2-2x-3;
(2)y=x2-2x-3=(x-1)2-4,
所以二次函数图象的顶点坐标为(1,-4).
根据题意得
|
|
所以二次函数解析式为y=x2-2x-3;
(2)y=x2-2x-3=(x-1)2-4,
所以二次函数图象的顶点坐标为(1,-4).
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数的性质.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
下列说法正确的是( )
A、
| ||
| B、无理数是无限小数 | ||
| C、无限小数是无理数 | ||
D、
|
等腰三角形的一个内角是70°,它的一腰上的高与底边的夹角是( )
| A、35°或110° |
| B、35°或20° |
| C、20°或55° |
| D、35°或55° |
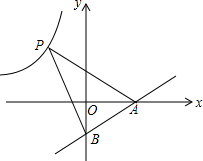 直线y=
直线y=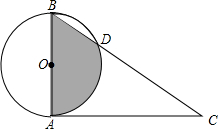 如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,∠C=30°.
如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,∠C=30°. 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.连接CE,连接DE交AC于F.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.连接CE,连接DE交AC于F. 已知,如图,在△ABC中,∠ABC=68°,∠ACB=50°,BE、CF是两边AC、AB
已知,如图,在△ABC中,∠ABC=68°,∠ACB=50°,BE、CF是两边AC、AB