题目内容
17.将二次函数y=$\frac{1}{2}$x2的图象向右平移2个单位,则所得抛物线的解析式为( )| A. | y=$\frac{1}{2}$(x-2)2 | B. | y=$\frac{1}{2}$(x+2)2 | C. | y=$\frac{1}{2}$x2-2 | D. | y=$\frac{1}{2}$x2+2 |
分析 抛物线y=$\frac{1}{2}$x2的顶点坐标为(0,0),向右平移2个单位,所得的抛物线的顶点坐标为(2,0),根据顶点式可确定所得抛物线解析式.
解答 解:依题意可知,二次函数y=$\frac{1}{2}$x2的图象的顶点坐标为(0,0),平移后抛物线顶点坐标为(2,0),
又因为平移不改变二次项系数,
∴所得抛物线解析式为:y=$\frac{1}{2}$(x-2)2.
故选:A.
点评 本题考查了二次函数图象与几何变换,属于基础题,解决本题的关键是得到新抛物线的顶点坐标.

练习册系列答案
相关题目
12.二次函数y=(x+2)2+1的顶点坐标是( )
| A. | (2,1) | B. | (-2,1) | C. | (-2,-l) | D. | (2,-l) |
2.已知在半径分别为4cm和7cm的两圆相交,则它们的圆心距可能是( )
| A. | 1cm | B. | 3cm | C. | 10cm | D. | 15cm |
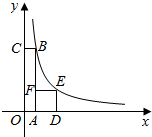 如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=$\frac{k}{x}$的图象上,OA=1,OC=6,则正方形ADEF的面积为( )
如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=$\frac{k}{x}$的图象上,OA=1,OC=6,则正方形ADEF的面积为( )