题目内容
7.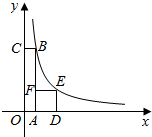 如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=$\frac{k}{x}$的图象上,OA=1,OC=6,则正方形ADEF的面积为( )
如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=$\frac{k}{x}$的图象上,OA=1,OC=6,则正方形ADEF的面积为( )| A. | 2 | B. | 4 | C. | 6 | D. | 12 |
分析 根据正方形的性质,设正方形ADEF的边长AD=t,则OD=1+t,则E点坐标为(1+t,t).代入反比例函数解析式即可求得t的值,得到正方形的边长.
解答 解:设正方形ADEF的边长AD=t,则OD=1+t.
∵四边形ADEF是正方形,
∴DE=AD=t.
∴E点坐标为(1+t,t).
∵E点在反比例函数y=$\frac{6}{x}$的图象上,
∴(1+t)•t=6.
整理,得 t2+t-6=0.
解得t1=-3,t2=2.
∵t>0,
∴t=2.
∴正方形ADEF的边长为2,
∴正方形ADEF的面积为4.
故选B.
点评 本题主要考查了正方形的性质和根据反比例函数的解析式列方程,求正方形的面积,这里体现了数形结合的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.将二次函数y=$\frac{1}{2}$x2的图象向右平移2个单位,则所得抛物线的解析式为( )
| A. | y=$\frac{1}{2}$(x-2)2 | B. | y=$\frac{1}{2}$(x+2)2 | C. | y=$\frac{1}{2}$x2-2 | D. | y=$\frac{1}{2}$x2+2 |
15.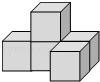 如图所示的几何体是由5个相同的小正方体组成的,下列有关三视图面积的说法中正确的是( )
如图所示的几何体是由5个相同的小正方体组成的,下列有关三视图面积的说法中正确的是( )
 如图所示的几何体是由5个相同的小正方体组成的,下列有关三视图面积的说法中正确的是( )
如图所示的几何体是由5个相同的小正方体组成的,下列有关三视图面积的说法中正确的是( )| A. | 左视图面积最大 | B. | 俯视图面积最小 | ||
| C. | 左视图与主视图面积相等 | D. | 俯视图与主视图面积相等 |
16.今年国庆节期间,峨眉山共接待游客约63.9万人次,较去年同期增长32.15%.63.9万用科学记数法表示为( )
| A. | 63.9×104 | B. | 0.639×106 | C. | 6.39×105 | D. | 6.39×106 |
 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论: