题目内容
5.在△ABC中,如果∠A、∠B满足,$|{tanA-1}|+{(sinB-\frac{1}{2})^2}=0$,则∠C=105°.分析 首先根据非负数的性质求出tanA和sinB的值,然后求出∠A、∠B的度数,继而可求得∠C的度数.
解答 解:由题意得,tanA=1,sinB=$\frac{1}{2}$,
则∠A=45°,∠B=30°,
故∠C=105°.
故答案为:105.
点评 本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15. 由如图通过平移后可以得到的图案是( )
由如图通过平移后可以得到的图案是( )
 由如图通过平移后可以得到的图案是( )
由如图通过平移后可以得到的图案是( )| A. |  | B. |  | C. |  | D. |  |
20.某公园门票价格规定如下表:
某校七年级(1)、(2)两个班104人去游园,其中七(1)班有40多人,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1138.问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七(1)班单独组织去游园,作为组织者的你将如何购票才最省钱?
| 购票张数 | 1-50张 | 51-100张 | 100张以上 |
| 每张票的价格 | 12元 | 10元 | 8元 |
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少钱?
(3)如果七(1)班单独组织去游园,作为组织者的你将如何购票才最省钱?
10.一次函数y=kx-k的大致图象可能如图( )
| A. |  | B. |  | C. |  | D. |  |
17.将二次函数y=$\frac{1}{2}$x2的图象向右平移2个单位,则所得抛物线的解析式为( )
| A. | y=$\frac{1}{2}$(x-2)2 | B. | y=$\frac{1}{2}$(x+2)2 | C. | y=$\frac{1}{2}$x2-2 | D. | y=$\frac{1}{2}$x2+2 |
14.若点A(x1,y1)和点B(x2,y2)在正比例函数y=-3x的图象上,当x1<x2时,y1与y2的大小关系为( )
| A. | y1>y2 | B. | y1<y2 | ||
| C. | y1=y2 | D. | y1与y2的大小不一定 |
15.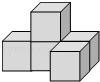 如图所示的几何体是由5个相同的小正方体组成的,下列有关三视图面积的说法中正确的是( )
如图所示的几何体是由5个相同的小正方体组成的,下列有关三视图面积的说法中正确的是( )
 如图所示的几何体是由5个相同的小正方体组成的,下列有关三视图面积的说法中正确的是( )
如图所示的几何体是由5个相同的小正方体组成的,下列有关三视图面积的说法中正确的是( )| A. | 左视图面积最大 | B. | 俯视图面积最小 | ||
| C. | 左视图与主视图面积相等 | D. | 俯视图与主视图面积相等 |
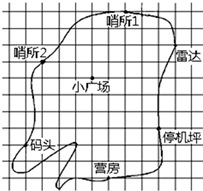 南海诸岛自古以来就是中华民族神圣领土的一部分,我国对南海诸岛及其附近海域拥有无可争辩的主权.如图是我国南沙群岛中某个小岛的平面示意图,小明建立了平面直角坐标系后,营房的坐标为(2,-5),哨所2的坐标为(-2,2).
南海诸岛自古以来就是中华民族神圣领土的一部分,我国对南海诸岛及其附近海域拥有无可争辩的主权.如图是我国南沙群岛中某个小岛的平面示意图,小明建立了平面直角坐标系后,营房的坐标为(2,-5),哨所2的坐标为(-2,2).