题目内容
 己知:如图,⊙D交y轴于A、B,交x轴于C,过点C的直线
己知:如图,⊙D交y轴于A、B,交x轴于C,过点C的直线 与y轴交于P,D点坐标(0,1),求证:PC是⊙D的切线.
与y轴交于P,D点坐标(0,1),求证:PC是⊙D的切线.
证明:∵直线 交于x轴于点C,交y轴于P,
交于x轴于点C,交y轴于P,
∴点C,P坐标分别为( ),(0,-8).
),(0,-8).
∴OC= OP=8.
OP=8.
又∵∠COP=90°,
∴PC2=OC2+OP2,
∴PC=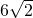 或
或 .
.
又∵ <0,
<0,
∴舍去.
∵点D坐标为(0,1),
∴DO=1.
又∵OC= ,∠DOC=90°,
,∠DOC=90°,
∴DC2=DO2+OC2=9.
∴DC=3或-3.
又∵-3<0,∴舍去.
又∵DO=1OP=8,
∴DP=9.
又∵DP2=81=72+9=PC2+DC2
∴∠DCP=90°.
即PC是⊙D的切线.
分析:已知直线 交于x轴于点C,交y轴于P,易得点C,P的坐标,然后根据勾股定理求出PC,DC的长.最后根据勾股定理推出PC是⊙D的切线.
交于x轴于点C,交y轴于P,易得点C,P的坐标,然后根据勾股定理求出PC,DC的长.最后根据勾股定理推出PC是⊙D的切线.
点评:本题主要考查的是一次函数的有关知识,同时要明确切线的判定定理作为突破口.
 交于x轴于点C,交y轴于P,
交于x轴于点C,交y轴于P,∴点C,P坐标分别为(
 ),(0,-8).
),(0,-8).∴OC=
 OP=8.
OP=8.又∵∠COP=90°,
∴PC2=OC2+OP2,
∴PC=
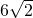 或
或 .
.又∵
 <0,
<0,∴舍去.
∵点D坐标为(0,1),
∴DO=1.
又∵OC=
 ,∠DOC=90°,
,∠DOC=90°,∴DC2=DO2+OC2=9.
∴DC=3或-3.
又∵-3<0,∴舍去.
又∵DO=1OP=8,
∴DP=9.
又∵DP2=81=72+9=PC2+DC2
∴∠DCP=90°.
即PC是⊙D的切线.
分析:已知直线
 交于x轴于点C,交y轴于P,易得点C,P的坐标,然后根据勾股定理求出PC,DC的长.最后根据勾股定理推出PC是⊙D的切线.
交于x轴于点C,交y轴于P,易得点C,P的坐标,然后根据勾股定理求出PC,DC的长.最后根据勾股定理推出PC是⊙D的切线.点评:本题主要考查的是一次函数的有关知识,同时要明确切线的判定定理作为突破口.

练习册系列答案
相关题目
 己知:如图,⊙D交y轴于A、B,交x轴于C,过点C的直线
己知:如图,⊙D交y轴于A、B,交x轴于C,过点C的直线
 (2012•上海)己知:如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G.
(2012•上海)己知:如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G. 与y轴交于P,D点坐标(0,1),求证:PC是⊙D的切线.
与y轴交于P,D点坐标(0,1),求证:PC是⊙D的切线.