��Ŀ����
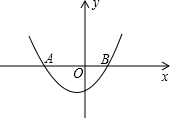
��֪����ͼ1��������y=ax2-2ax+c��a��0����y�ύ�ڵ�C��O��-4������x�ύ��A��B���㣬��A������Ϊ��4��0������1����������ߵĺ�������ʽ��
��2����P��t��O�����߶�AB��һ���㣨����A��B�غϣ�����P����PE��AC����BC��E������CP�����CPE�����S��t�ĺ�����ϵʽ����ָ��t��ȡֵ��Χ��
��3����ͼ2����ƽ����x��Ķ�ֱ��r��������߽��ڵ�Q����ֱ��AC����F����D������Ϊ��2��0�������Ƿ����������ֱ��r��ʹ�á�0DFΪ���������Σ������ڣ��������Q���ꣻ�������ڣ���˵�����ɣ�

��������!��A��C���������������ʽ���ɣ�
��2��ͨ�����Ʊ�ʾ��E�����꣬��������IJ����PEC�����
��3����ODFΪ���������Σ�û��ȷ�ױߣ�Ҫ�������ۣ����߶�������Q�����꣬Ȼ����������ߵĽ���ʽ��⣮
��2��ͨ�����Ʊ�ʾ��E�����꣬��������IJ����PEC�����
��3����ODFΪ���������Σ�û��ȷ�ױߣ�Ҫ�������ۣ����߶�������Q�����꣬Ȼ����������ߵĽ���ʽ��⣮
����⣺��1���������
��
���
��������ߵĺ�������ʽΪy=0.5x2-x-4��
��2������E��EG��x����G��
��0.5x2-x-4=0��
��x1=-2��x2=4��
AB=6��BP=2+t��
֤��BPE�ס�BAC���ɵ�EG=
��t+2����
S=S��CPB-S��BPE=
BP•CO-
BP•EG=
��t+2����4-
��t+2����=-
t2+
t+
-2��t��4��
��3��������Q����ڣ�ʹ�á�ODFΪ���������Σ�
�ٵ�OF=DFʱ��Q��x��-3��
0.5x2-x-4=-3��x=1��
��
��Q1(1+
��-3)��Q2(1-
��-3)
�ڵ�OD=DF=2ʱ��Q��x��-2��
0.5x2-x-4=-2��x=1��
��
��Q3(1+
��-2)��Q4(1-
��-2)��
|
���
|
��������ߵĺ�������ʽΪy=0.5x2-x-4��
��2������E��EG��x����G��

��0.5x2-x-4=0��
��x1=-2��x2=4��
AB=6��BP=2+t��
֤��BPE�ס�BAC���ɵ�EG=
| 2 |
| 3 |
S=S��CPB-S��BPE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
-2��t��4��
��3��������Q����ڣ�ʹ�á�ODFΪ���������Σ�
�ٵ�OF=DFʱ��Q��x��-3��
0.5x2-x-4=-3��x=1��
| 3 |
��Q1(1+
| 3 |
| 3 |
�ڵ�OD=DF=2ʱ��Q��x��-2��
0.5x2-x-4=-2��x=1��
| 5 |
��Q3(1+
| 5 |
| 5 |
�������ٵ���ͼ���������������������ʽ����û�б����������ϵ������������Ҫת���������ü���ͼ�η��࣮

��ϰ��ϵ�д�
�����Ŀ
 ���ʣ��Ƿ����ʵ��k��ʹ��AOC���COB���ƣ������ڣ������Ӧ��k��ֵ���������ڣ���˵�����ɣ�
���ʣ��Ƿ����ʵ��k��ʹ��AOC���COB���ƣ������ڣ������Ӧ��k��ֵ���������ڣ���˵�����ɣ�

