题目内容
 如图,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕,∠C=130°,则∠AEB的度数为
如图,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕,∠C=130°,则∠AEB的度数为考点:翻折变换(折叠问题)
专题:
分析:根据四边形的内角和等于360°求出∠BAD,根据翻折的性质可得∠BAE=∠DAE,然后求出∠BAE,再根据直角三角形两锐角互余列式计算即可得解.
解答:解:∵∠B=∠D=90°,∠C=130°,
∴∠BAD=360°-90°×2-130°=50°,
由翻折的性质得,∠BAE=∠DAE,
∴∠BAE=
∠BAD=
×50°=25°,
∵∠B=90°,
∴∠AEB=90°-25°=65°.
故答案为:65°.
∴∠BAD=360°-90°×2-130°=50°,
由翻折的性质得,∠BAE=∠DAE,
∴∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠B=90°,
∴∠AEB=90°-25°=65°.
故答案为:65°.
点评:本题考查了翻折变换的性质,四边形的内角和定理,直角三角形两锐角互余的性质.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
在平面直角坐标系xOy中,若点P在第四象限,且点P到x轴的距离为1,到y轴的距离为
,则点P的坐标为( )
| 5 |
A、(
| ||
B、(-
| ||
C、(1,-
| ||
D、(-1,
|
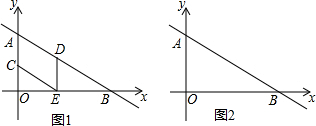 如图,在平面直角坐标系中,直线y=-
如图,在平面直角坐标系中,直线y=-