题目内容
6.在Rt△ABC中,∠C=90°,且∠A,∠B,∠C的对边分别为a,b,c.(1)已知c=6,∠A=60°,则a=3,b=3$\sqrt{3}$;
(2)已知a=4,∠B=45°,则b=4,c=4$\sqrt{2}$.
分析 (1)首先根据斜边的长和∠A的度数求得b的长,然后利用勾股定理求得a的长即可;
(2)根据直角边的长和∠B的长,然后求得另一条直角边的长,从而求得斜边的长.
解答 解:(1)∵c=6,∠A=60°,
∴$\frac{b}{c}$=cosA,
即:b=c×cosA=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
a=$\sqrt{{c}^{2}-{b}^{2}}$=$\sqrt{36-27}$=3;
(2)∵a=4,∠B=45°,
∴b=a=4,
c=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
故答案为:3,3$\sqrt{3}$;4,4$\sqrt{2}$.
点评 考查了解直角三角形的知识,解题的关键是能够选择合适的边角关系,难度不大.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
17.圆的半径为13cm,两弦AB∥CD,AB=24cm,CD=10cm,则两弦AB,CD的距离是( )
| A. | 7cm | B. | 17cm | C. | 12cm | D. | 7cm或17cm |
1.甲、乙两地相距100km,一辆汽车从甲地到乙地,则关于汽车到达乙地所用的时间t(h)与汽车的平均速度v(km/h)的函数图象说法正确的是( )
| A. | 图象在第一、三象限 | B. | 图象在第二、四象限 | ||
| C. | 图象在第一象限 | D. | 图象在第三象限 |
15.A(-3,2)关于y轴的对称点是B,B关于x轴的对称点是C,则点C的坐标是( )
| A. | (-2,3) | B. | (-3,2) | C. | (3,-2) | D. | (3,2) |
16.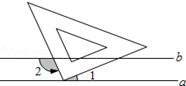 如图,小华把三角板的直角顶点放在直线a上,两条直角边与直线b相交,如果a∥b,且∠1=40°,则∠2的度数为( )
如图,小华把三角板的直角顶点放在直线a上,两条直角边与直线b相交,如果a∥b,且∠1=40°,则∠2的度数为( )
 如图,小华把三角板的直角顶点放在直线a上,两条直角边与直线b相交,如果a∥b,且∠1=40°,则∠2的度数为( )
如图,小华把三角板的直角顶点放在直线a上,两条直角边与直线b相交,如果a∥b,且∠1=40°,则∠2的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
 如图,如果AC∥BD,CE∥DF,那么△ACE与△BDF是否相似?△ACE与△BDF是否位似?试说明理由.
如图,如果AC∥BD,CE∥DF,那么△ACE与△BDF是否相似?△ACE与△BDF是否位似?试说明理由.