题目内容
(1)解方程:
-
=1
(2)先化简,再求值:(
+
)÷
,其中x=-2,y=1.
| 2x |
| 2x-5 |
| 1 |
| 2x+5 |
(2)先化简,再求值:(
| 1 |
| x+y |
| 1 |
| y-x |
| y2 |
| xy-y2 |
考点:分式的化简求值,解分式方程
专题:
分析:(1)首先找出最简公分母,进而去分母解方程即可;
(2)首先进行通分运算,进而化简求出即可.
(2)首先进行通分运算,进而化简求出即可.
解答:解:(1)
-
=1
去分母得:
2x(2x+5)-(2x-5)=(2x-5)(2x+5)
解得;x=-
,
检验得:x=-
是原方程的根;
(2)(
+
)÷
,
=[
-
]×
=
×
=-
将x=-2,y=1代入得:
原式=-
=2.
| 2x |
| 2x-5 |
| 1 |
| 2x+5 |
去分母得:
2x(2x+5)-(2x-5)=(2x-5)(2x+5)
解得;x=-
| 15 |
| 4 |
检验得:x=-
| 15 |
| 4 |
(2)(
| 1 |
| x+y |
| 1 |
| y-x |
| y2 |
| xy-y2 |
=[
| x-y |
| (x+y)(x-y) |
| x+y |
| (x+y)(x-y) |
| y(x-y) |
| y2 |
=
| -2y |
| (x+y)(x-y) |
| y(x-y) |
| y2 |
=-
| 2 |
| x+y |
将x=-2,y=1代入得:
原式=-
| 2 |
| -2+1 |
点评:此题主要考查了分式的混合运算以及解分式方程,正确化简分式是解题关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
给出以下五种说法:
①若a,b,c为实数,且a>b,则ac2>bc2;
②用有序数对或方位和距离可以确定物体的具体位置;
③命题“三角形一条边的两个顶点到这条边上的中线所在直线的距离相等”是真命题;
④如果一个等腰三角形的两边长为4cm和9cm,那么它的周长是17cm或22cm;
⑤如果关于x的不等式-k-x+6>0的正整数解为1,2,3,那么k应取值为2≤k<3.
其中说法正确的是( )
①若a,b,c为实数,且a>b,则ac2>bc2;
②用有序数对或方位和距离可以确定物体的具体位置;
③命题“三角形一条边的两个顶点到这条边上的中线所在直线的距离相等”是真命题;
④如果一个等腰三角形的两边长为4cm和9cm,那么它的周长是17cm或22cm;
⑤如果关于x的不等式-k-x+6>0的正整数解为1,2,3,那么k应取值为2≤k<3.
其中说法正确的是( )
| A、①②⑤ | B、②③⑤ |
| C、②③④ | D、①②④⑤ |
关于x的不等式组
的解集在同一数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
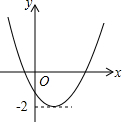 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0有实数根,下列结论:①abc>0;②b2-4ac>0;③m>-2,其中,正确的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0有实数根,下列结论:①abc>0;②b2-4ac>0;③m>-2,其中,正确的个数是( )| A、0 | B、1 | C、2 | D、3 |
 如图,A、B两点在双曲线y=
如图,A、B两点在双曲线y=| 4 |
| x |
| A、4 | B、2 | C、1 | D、无法确定 |