Question

【题目】如图1，平面直角坐标系中，的边在轴的正半轴上，点在第二象限，且，，，抛物线经过点，并与轴交于点，点在抛物线的对称轴上．

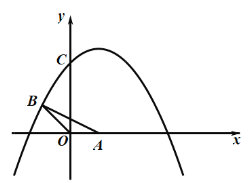
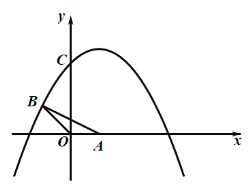
（图1） （备用图）

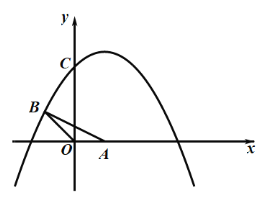
（备用图）

（1）求、的值，及抛物线的对称轴．

（2）求证：以点为圆心，半径为的圆与边相切．

（3）若满足条件与的点恰好在抛物线上，请求出此时点的坐标．

Answer 1

【答案】（1）b=1,c=5,x=2；（2）见详解；（3）P（2，－2＋2）、P（2，－2－2）、P（2，4）、P（2，－8）.

【解析】

（1）根据已知的∠AOB＝135°，可知点B的横纵坐标互为相反数，再根据OB的长度，即可求得点B的坐标；

（2）作MK⊥AB于点K ，作BG⊥OA于G，利用△MKA与△AGB相似，可求得圆心到直线AB的距离，从而是否判断相切；

（3）由题意可知∠POD＝45°，OD＝OP，因此通过构造直角三角形可以求得.

：（1）由题意得c＝5，点B（2，－2），

把点B（2，－2）代入中，得b＝1，

对称轴.

（2）如图，作MK⊥AB于K，作BG⊥OA于G，

∵△MKA∽△AGB，

∴，

∴，

MK＝2，

∵r＝2，

∴d＝r＝2，

∴⊙M与相切.

（3）∵∠AOB＋∠POD＝180°，∠AOB＝135°，

∴∠POD＝45°

∵OB：OD＝OA：OP，

∴OD：OP＝OB：OA＝，

①当点P在如图所示位置时，

过点P作DP⊥OP于点P，则PD＝OP，再作DH⊥AP于点H ，则△DHP≌△PAO，

∴DH＝AP，HP＝OA

设P（2，m），则D（2－m，m＋2），

∵D在y＝x2＋x＋5上，

∴ m＋2＝（2﹣m）2＋2﹣m＋5，

解得m＝﹣2＋2，或﹣2＋2（舍去）

此时P（2，﹣2＋2）或（2，﹣2﹣2），

②当点P在如图所示位置时，

与①同理，△OAP≌△PHD，则HD＝AP，HP＝OA，

设P（2，m），则D（2＋m，m﹣2），

∵D在y＝x2＋x＋5上，

∴m﹣2＝（2＋m）2＋2＋m＋5，

解得m＝﹣8或4．

此时P（2，﹣8）或（2，4），

综上所述，满足条件的点P的坐标为（2，﹣2＋2）或（2，﹣2﹣2）或（2，﹣8）或（2，4）．