题目内容
1.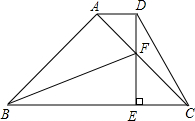 如图,已知在梯形ABCD中,AD∥BC,DE⊥BC于点E,交AC于点F,∠ACB=45°,连接BF,∠FBC=∠EDC.
如图,已知在梯形ABCD中,AD∥BC,DE⊥BC于点E,交AC于点F,∠ACB=45°,连接BF,∠FBC=∠EDC.(1)求证:BF=CD;
(2)若AB=5,BC=7,求梯形ABCD的面积.
分析 (1)过点A作AG⊥BC于G,由∠ACB=45°,DE⊥BC,得到等腰直角三角形,得到边相等,证得全等三角形,得到对应边相等;
(2)根据梯形的底平行,DE⊥BC,得到等腰直角三角形,证得矩形,得到对边相等,由等腰直角三角形的直角边相等,通过等量代换,得到线段相等,由勾股定理列方程求所需线段的才长度,根据梯形的面积公式求得结果.
解答 解:(1)过点A作AG⊥BC于G,
∵DE⊥BC,
∴∠DEB=∠DEC=90°
∵∠ACB=45°
∴EF=EC,
∵∠FBC=∠EDC,
在△BEF与△DEC中,$\left\{\begin{array}{l}{∠DEC=∠BEF}\\{∠EDC=∠BFE}\\{EF=CE}\end{array}\right.$,
∴△DEC≌△BEF(AAS)
∴BF=CD;
(2)∵AD∥BC,DE⊥BC,
∴∠EDA=90°,∠DAC=∠ACB=45°,
∴AD=DF,
∵AG⊥BC
∴四边形ADEG是矩形,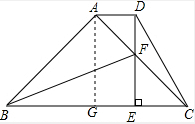
∴EG=AD,AG=DE,
∴EG=DF,AG=BE,
∵AG⊥BC,∠ACB=45°,
∴AG=CG,
∴BE=CG,
∵BE=BG+EG,CG=CE+EG,
∴BG=CE,
设CE=x,则BG=x,
∵BC=7,
∴BE=BC-CE=7-x,
∴AG=BE=7-x,
∵AB2=AG2+BG2,AB=5,∴52=x2+(7-x)2,
解得x=3和x=4(因2x=8>7故舍去x=4)
∴AG=7-x=4,EG=7-2x=1,
∴AD=1,
∴S梯形=(AD+BC)×AG/2=(1+7)×4/2=16.
点评 本题考查了等腰直角三角形的判定和性质,矩形的判定和性质,全等三角形的判定与性质,勾股定理得应用,梯形的面积公式等知识点.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
1.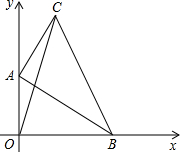 如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )
如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )
 如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )
如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )| A. | 5 | B. | 2+$\sqrt{13}$ | C. | $\sqrt{13}$ | D. | 6 |
10.下列各式的值最小的是( )
| A. | 0-3 | B. | -22 | C. | -4×0 | D. | |-5| |
 如图,在直角坐标系中,矩形ABCD的边OA在x轴上,边OC在y轴上,点B的坐标为(3,4),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{12}{5}$,$\frac{16}{5}$).
如图,在直角坐标系中,矩形ABCD的边OA在x轴上,边OC在y轴上,点B的坐标为(3,4),直线CD分别交OB、AB于点D、E,若BD=BE,则点D的坐标为($\frac{12}{5}$,$\frac{16}{5}$). 如图,Rt△ABC中,∠ACB=90°,AC=BC,Rt△DEF中,∠DFE=90°,D、E两点分别在AC、BC上,且DE=BC.若∠CFB=135°,CF=1,EF=3,则AB=5$\sqrt{2}$.
如图,Rt△ABC中,∠ACB=90°,AC=BC,Rt△DEF中,∠DFE=90°,D、E两点分别在AC、BC上,且DE=BC.若∠CFB=135°,CF=1,EF=3,则AB=5$\sqrt{2}$.