题目内容
10. 下列能判定AB∥CD的条件有( )个.
下列能判定AB∥CD的条件有( )个.①∠B+∠BCD=180°;
②∠1=∠2;
③∠3=∠4;
④∠B=∠D.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据平行线的判定定理进行解答.
解答 解:①∵∠B+∠BDC=180°,∴AB∥CD(同旁内角互补,两直线平行),能判定AB∥CD,故错误;
②∠1与∠2是直线AC、BD被AD所截形成的内错角,因为∠1=∠2,所以应是AC∥BD,不能判定AB∥CD,故正确;
③∵∠3=∠4,∴AB∥CD (内错角相等,两直线平行),能判定AB∥CD,故错误;
④∠B=∠D,不能判定AB∥CD,故正确;
故选:B.
点评 本题考查了平行线的判定.解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养学生“执果索因”的思维方式与能力.

练习册系列答案
相关题目
3.如果l1∥l2,l2∥l3,那么l1与l3的关系是( )
| A. | 平行 | B. | 相交 | C. | 重合 | D. | 不能确定 |
19.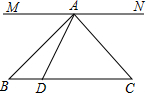 如图,在△ABC中,点D是BC边上一点且CD=CA,过点A作MN∥BC,∠CAN=48°,∠B=41°,∠BAD=( )
如图,在△ABC中,点D是BC边上一点且CD=CA,过点A作MN∥BC,∠CAN=48°,∠B=41°,∠BAD=( )
 如图,在△ABC中,点D是BC边上一点且CD=CA,过点A作MN∥BC,∠CAN=48°,∠B=41°,∠BAD=( )
如图,在△ABC中,点D是BC边上一点且CD=CA,过点A作MN∥BC,∠CAN=48°,∠B=41°,∠BAD=( )| A. | 23° | B. | 24° | C. | 25° | D. | 26° |
2. 如图,若直线a∥b,那么∠x=( )
如图,若直线a∥b,那么∠x=( )
 如图,若直线a∥b,那么∠x=( )
如图,若直线a∥b,那么∠x=( )| A. | 64° | B. | 68° | C. | 69° | D. | 66° |
19.两个袋子里分别装着写有1,2,3,4的四张完全相同的卡片,从每一袋子中各随机抽取一张,则两张卡片上数字之和等于6的概率是( )
| A. | $\frac{1}{16}$ | B. | $\frac{2}{16}$ | C. | $\frac{3}{16}$ | D. | $\frac{1}{2}$ |
17.若代数式2x2+3x-7的值是6,则代数式7-3x-2x2的值是( )
| A. | 6 | B. | -6 | C. | -7 | D. | 7 |
 如图,在平面直角坐标系中,⊙A与x轴相切于点B,BC为⊙A的直径,点C在函数y=$\frac{k}{x}$的图象上.若△OAB的面积为3,则k的值为( )
如图,在平面直角坐标系中,⊙A与x轴相切于点B,BC为⊙A的直径,点C在函数y=$\frac{k}{x}$的图象上.若△OAB的面积为3,则k的值为( )