题目内容
14.若(2x-1)3=a+bx+cx2+dx3,求a+b+c+d的值,可令x=1,得:(2×1-1)3=a+b+c+d,所以a+b+c+d=1.上述条件不变,利用上面的方法,
(1)求a的值;
(2)能否求出a+c的值?若能,请写出解答过程;若不能,请说明理由.
分析 (1)令x=0即可确定出a的值;
(2)令x=-1得到关系式,与a+b+c+d的值联立求出a+c的值即可.
解答 解:(1)令x=0,则(2×0-1)3=a,
∴a=-1;
(2)能求出a+c的值,
令x=-1,得[2×(-1)-1]3=a-b+c-d,
∴(a+c)-(b+d)=-27,
∵a+b+c+d=1,
∴b+d=1-(a+c),
∴(a+c)-[1-(a+c)]=-27,
2(a+c)=-26,
∴a+c=-13.
点评 此题考查了代数式求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
4.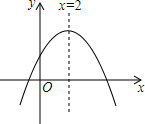 二次函数y=ax2+bx+c的图象如图所示,若点A(-1,y1),B(-2,y2)是其图象上的两点,则y1与y2的大小关系是( )
二次函数y=ax2+bx+c的图象如图所示,若点A(-1,y1),B(-2,y2)是其图象上的两点,则y1与y2的大小关系是( )
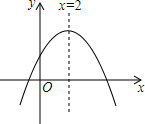 二次函数y=ax2+bx+c的图象如图所示,若点A(-1,y1),B(-2,y2)是其图象上的两点,则y1与y2的大小关系是( )
二次函数y=ax2+bx+c的图象如图所示,若点A(-1,y1),B(-2,y2)是其图象上的两点,则y1与y2的大小关系是( )| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
9.使分式$\frac{2}{x-3}$有意义的x的取值范围是( )
| A. | x≠3 | B. | x>3 | C. | x<3 | D. | x=3 |
 如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.
如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.