题目内容
4．
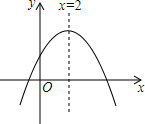二次函数y=ax2+bx+c的图象如图所示，若点A（-1，y1），B（-2，y2）是其图象上的两点，则y1与y2的大小关系是（ ）| A． | y1＞y2 | B． | y1=y2 | C． | y1＜y2 | D． | 无法确定 |
分析 利用函数图象可判断点A（-1，y1），B（-2，y2）都在直线x=2左侧的抛物线上，然后根据二次函数的性质可判断y1与y2的大小．
解答 解：∵抛物线的对称轴为直线x=2，
∴点A（-1，y1），B（-2，y2）都在直线x=2左侧的抛物线上，
∴y1＞y2．
故选A．
点评 本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．解决本题的关键是判断点A和点B都在对称轴的左侧．
练习册系列答案
阅读快车系列答案
相关题目
15．在平面直角坐标系中，已知点P的坐标是（-1，-2），则点P关于y轴对称的点的坐标是（ ）
| A． | （-1，2） | B． | （1，-2） | C． | （1，2） | D． | （2，1） |
如图所示的“杨辉三角”告诉了我们二项式乘方展开式的系数规律，如：第三行的三个数（1、2、1）恰好对应着（a+b）2的展开式a2+2ab+b2的系数；第四行的四个数恰好对应着（a+b）3=a3+3a2b+3ab2+b3的系数，根据数表中前五行的数字所反映的规律，回答：
19．
如图，若△ABC中，∠C=90°，AD平分∠BAC，CD=3cm，AB=10cm，则△ABD的面积是（ ）
如图，若△ABC中，∠C=90°，AD平分∠BAC，CD=3cm，AB=10cm，则△ABD的面积是（ ）| A． | 15cm2 | B． | 10cm2 | C． | 5cm2 | D． | 2.5cm2 |
9．若-$\frac{{5a}^{3}{b}^{n+2}}{2}$是一个5次单项式，则n的值是（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
16．下列各组中的两个分式不相等的是（ ）
| A． | $\frac{2x}{y}$与$\frac{4xy}{{2y}^{2}}$ | B． | $\frac{-2{mn}^{2}}{{4m}^{2}n}$与-$\frac{n}{2m}$ | ||
| C． | $\frac{-5y}{-2{5x}^{2}}$与$\frac{y}{{5x}^{2}}$ | D． | $\frac{{y}^{2}-{x}^{2}}{{（x-y）}^{2}}$与$\frac{x+y}{x-y}$ |