题目内容
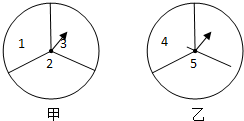王敏想设计甲、乙两个转盘，通过转转盘来决定张祥与李明谁能得到一张演唱会的门票，每个转盘被分成面积相等的三个扇形区域，并在每个区域内标上不同的数字，数字在1、2、3、4、5、6、7中选，每个数字只能选用一次，转盘甲已经设计好，转盘乙还有一个数字未填．（1）当转盘乙未填的数字为
（2）若转转盘的规则为：同时转动两个转盘，当转盘停止转动后，指针所指扇形区域内数字的和为偶数时，则张祥胜；否则李明胜（如指针在分割线上，则重新转动转盘）．问王敏能设计出对张祥与李明均公平的转盘吗？若能，未填的数字应填6还是7？若不能，试说明理由．
考点：列表法与树状图法
专题：计算题
分析：（1）列表得出所有等可能的情况，分选择6和7分别求出概率，比较即可；
（2）不能，理由为：分选择6和7分别求出两人获胜的概率，比较即可．
（2）不能，理由为：分选择6和7分别求出两人获胜的概率，比较即可．
解答：解：（1）若选择6，列表如下：
所有等可能的情况有9种，其中之和为7的有3种，P（之和为7）=
=
；
若选择7，列表如下：
所有等可能的情况有9种，其中之和为7的有2种，P（之和为7）=
；
则当转盘乙未填的数字为6时，指针所指两个扇形区域内数字的和为7的概率最大；
故答案为：6；
（2）不能，理由为：
若选择6，所有等可能的情况有9种，其中之和为偶数的情况有4种，之和为奇数的情况有5种，
张翔与李明获胜概率不相同，故不公平；
若选择7，所有等可能的情况有9种，其中之和为偶数的情况有4种，之和为奇数的情况有5种，
张翔与李明获胜概率不相同，故不公平．
| 1 | 2 | 3 | |
| 4 | （4，1） | （4，2） | （4，3） |
| 5 | （5，1） | （5，2） | （5，3） |
| 6 | （6，1） | （6，2） | （6，3） |
| 3 |
| 9 |
| 1 |
| 3 |
若选择7，列表如下：
| 1 | 2 | 3 | |
| 4 | （4，1） | （4，2） | （4，3） |
| 5 | （5，1） | （5，2） | （5，3） |
| 7 | （7，1） | （7，2） | （7，3） |
| 2 |
| 9 |
则当转盘乙未填的数字为6时，指针所指两个扇形区域内数字的和为7的概率最大；
故答案为：6；
（2）不能，理由为：
若选择6，所有等可能的情况有9种，其中之和为偶数的情况有4种，之和为奇数的情况有5种，
张翔与李明获胜概率不相同，故不公平；
若选择7，所有等可能的情况有9种，其中之和为偶数的情况有4种，之和为奇数的情况有5种，
张翔与李明获胜概率不相同，故不公平．
点评：此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
名校课堂系列答案
相关题目
如果不等式组
恰有3个整数解，则a的取值范围是（ ）
|
| A、a≤-1 |
| B、a＜-1 |
| C、-2≤a＜-1 |
| D、-2＜a≤-1 |
画出如图的几何体的三视图．
如图，⊙O1与⊙O2外切于点D，直线l与两圆分别相切于点A、B，与直线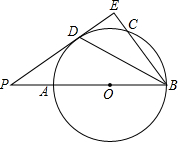
如图，在⊙O中，点P为直径BA延长线上一点，直线PD切⊙O于点D，过点B作BE⊥PD，垂足为E，BE交⊙O于点C，连接BD．