题目内容
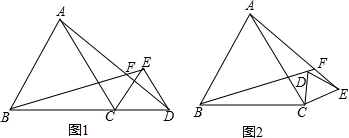
(1)如图1,C为线段BD上的一个动点(不与点B、D重合),在BD同侧分别作等边△ABC和等边△CDE,AD与BE相交于点F,求证:△ACD≌△BCE.
(2)将△CDE绕C点旋转至如图2,在旋转过程中,∠AFB的大小是否发生改变?若不改变,请求出∠AFB的度数;若改变,请说明理由.
【考点】全等三角形的判定与性质;等边三角形的性质.
【分析】(1)根据等边三角形的性质得到AC=BC,CE=CD,∠ACB=∠DCE=60°,求得∠BCE=∠ACD,即可得到结论;
(2)根据等边三角形的性质得到AC=BC,CE=CD,∠ACB=∠DCE=60°,推出△ACE≌△BCD,由全等三角形的性质得到∠CAF=∠CBF,由对顶角相等得到∠AOF=∠BOC,即可得到结论.
【解答】(1)证明:在等边△ABC和等边△CDE中,
∵AC=BC,CE=CD,∠ACB=∠DCE=60°,
∴∠BCE=∠ACD,
在△BCE与△ACD中,
 ,
,
∴△ACD≌△BCE;
(2)不改变,
理由:在等边△ABC和等边△CDE中,
∵AC=BC,CE=CD,∠ACB=∠DCE=60°,
∴∠BCE=∠ACD,
在△BCD与△ACE中,
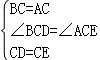 ,
,
∴△ACE≌△BCD,
∴∠CAF=∠CBF,
∵∠AOF=∠BOC,
∴∠AFB=∠ACB=60°,
∴∠AFB的大小不发生改变.

【点评】本题考查了全等三角形的判定和性质,等边三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目

 的最简公分母是( )
的最简公分母是( )