题目内容
1.解方程(1)x2-10x+9=0(配方法)
(2)(2x-5)2-4(3x-1)2=0.
分析 (1)把常数项移到右边,两边加上一次项系数一半的平方,左边配成完全平方的形式,再用直接开平方求出方程的根.
(2)利用平方差公式因式分解法解方程.
解答 解:(1)x2-10x=-9,
x2-10x+25=16,
(x-5)2=16,
x-5=±4,
解得:x1=1,x2=9.
(2)(2x-5)2-4(3x-1)2=0,
(2x-5+6x-2)(2x-5-6x+2)=0,
(8x-7)(-4x-3)=0,
8x-7=0,-4x-3=0,
解得:x1=$\frac{7}{8}$,x2=-$\frac{3}{4}$.
点评 本题考查了解一元二次方程,掌握解方程的方法与步骤是解决问题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
13. 如图,在数轴上表示1、$\sqrt{2}$的点分别为A、B,点B关于点A的对称点为C,则C点所表示的是( )
如图,在数轴上表示1、$\sqrt{2}$的点分别为A、B,点B关于点A的对称点为C,则C点所表示的是( )
 如图,在数轴上表示1、$\sqrt{2}$的点分别为A、B,点B关于点A的对称点为C,则C点所表示的是( )
如图,在数轴上表示1、$\sqrt{2}$的点分别为A、B,点B关于点A的对称点为C,则C点所表示的是( )| A. | 2-$\sqrt{2}$ | B. | $\sqrt{2}$-2 | C. | 1-$\sqrt{2}$ | D. | $\sqrt{2}$-1 |
10. 如图,平面上到两两相交的三条直线a、b、c的距离都相等的点一共有( )
如图,平面上到两两相交的三条直线a、b、c的距离都相等的点一共有( )
 如图,平面上到两两相交的三条直线a、b、c的距离都相等的点一共有( )
如图,平面上到两两相交的三条直线a、b、c的距离都相等的点一共有( )| A. | 1个 | B. | 4个 | C. | 2个 | D. | 3个 |
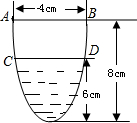 一个横断面是抛物线的渡槽如图所示,根据图中所给的数据求出水面的宽度是2$\sqrt{3}$cm.
一个横断面是抛物线的渡槽如图所示,根据图中所给的数据求出水面的宽度是2$\sqrt{3}$cm.