题目内容
 如图是抛物线拱桥,已知水位在AB位置时,水面宽4
如图是抛物线拱桥,已知水位在AB位置时,水面宽4 米,水面距离桥顶12米,当水位上升达到警戒线CD时水面宽4
米,水面距离桥顶12米,当水位上升达到警戒线CD时水面宽4 米,若洪水到来时,水位以每小时0.25米速度上升.
米,若洪水到来时,水位以每小时0.25米速度上升.
(1)建立适当的平面直角坐标系,求该抛物线的解析式.
(2)求水过警戒线后几小时淹到拱桥顶?
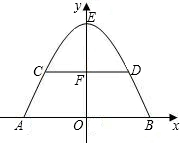
 解:(1)以拱桥最高点为坐标原点,建立直角坐标系,
解:(1)以拱桥最高点为坐标原点,建立直角坐标系,设y=ax2,
∵AB=4
 ,故B点坐标(2
,故B点坐标(2 ,-12),
,-12),∴-12=24a,
∴a=-
 ,
,∴y=-
 x2,
x2,(2)由题意得 C(-2
 ,y1) D(2
,y1) D(2 ,y2)
,y2) 将D(2
 ,y2)代入,得y2=-6
,y2)代入,得y2=-6 ∴t=
 =24,
=24,故水过警戒线后24小时淹到拱桥顶.
分析:(1)以拱桥最高点为坐标原点,建立直角坐标系,设y=ax2,求得a,(2)求D点的纵坐标,由t=
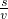 可得时间.
可得时间.点评:本题主要考查二次函数的应用,运用二次函数解决实际问题,比较简单.

练习册系列答案
相关题目
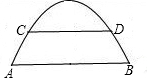 如图是抛物线拱桥,已知水位在AB位置时,水面宽4
如图是抛物线拱桥,已知水位在AB位置时,水面宽4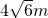 ,水位上升3m,达到警戒线CD,这时水面宽
,水位上升3m,达到警戒线CD,这时水面宽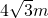 .若洪水到来时,水位以每小时0.25m的速度上升,求水过警戒线后几小时淹到拱桥顶?
.若洪水到来时,水位以每小时0.25m的速度上升,求水过警戒线后几小时淹到拱桥顶?
 ,水位上升3m,达到警戒线CD,这时水面宽
,水位上升3m,达到警戒线CD,这时水面宽 .若洪水到来时,水位以每小时0.25m的速度上升,求水过警戒线后几小时淹到拱桥顶?
.若洪水到来时,水位以每小时0.25m的速度上升,求水过警戒线后几小时淹到拱桥顶?