题目内容
6．计算：（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）…（1-$\frac{1}{{9}^{2}}$）（1-$\frac{1}{1{0}^{2}}$）…（1-$\frac{1}{{n}^{2}}$）=$\frac{n+1}{2n}$．分析 直接利用平方差公式将原式变形进而计算得出答案．
解答 解：（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）…（1-$\frac{1}{{9}^{2}}$）（1-$\frac{1}{1{0}^{2}}$）…（1-$\frac{1}{{n}^{2}}$）
=（1+$\frac{1}{2}$）×（1-$\frac{1}{2}$）×（1+$\frac{1}{3}$）×（1-$\frac{1}{3}$）×（1+$\frac{1}{4}$）×（1-$\frac{1}{4}$）…×（1+$\frac{1}{n}$）（1-$\frac{1}{n}$）
=$\frac{3}{2}$×$\frac{1}{2}$×$\frac{4}{3}$×$\frac{2}{3}$×$\frac{3}{4}$×$\frac{5}{4}$…×$\frac{n-1}{n}$×$\frac{n+1}{n}$
=$\frac{1}{2}$×$\frac{n+1}{n}$
=$\frac{n+1}{2n}$．
故答案为：$\frac{n+1}{2n}$．
点评 此题主要考查了平方差公式，正确将原式变形是解题关键．
练习册系列答案
相关题目
已知正方形OABC的边长为a，如图，以O为坐标原点，OA，OC所在直线为坐标轴建立直角坐标系，直线AB、CB与反比例函数y=$\frac{k}{x}$（k＞0）图象交于P，Q两点，连接OP，OQ，PQ．若a=4，且BP=AP，则k=8；若k=8$\sqrt{3}$，且∠POQ＜30°，则边长a的取值范围是$\sqrt{8\sqrt{3}}$＜a＜2$\sqrt{6}$．
如图，平面直角坐标系中，直线y=x+2与x轴交于点A，与y轴交于点D，B为AO的中点，DC⊥DB交x轴于点C，E在y轴上，且OC=OE，经过B、E、C三点的抛物线与直线AD交于F、G两点，与其对称轴交于M点
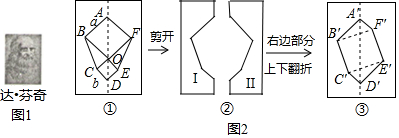
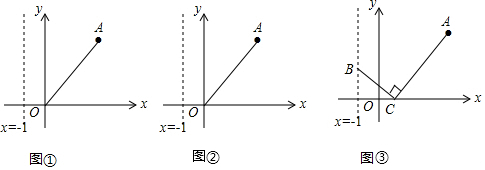
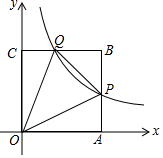
11．无论m为何值，点A（m，3-2m）不可能在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
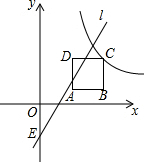边长为a的正方形ABCD在平面直角坐标系中的位置如图所示，其中AB与x轴平行（点B在点A的右侧），点A的坐标为（2，1），反比例函数y=$\frac{m}{x}$经过点C，直线l：y=kx-2（k≠0）与y轴交于点E．
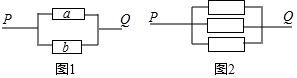在物理实验中，当电流在一定时间段内正常通过电子元件时，每个电子元件的状态有两种可能；通电或断开，并且这种状态的可能性相等．