题目内容
20.如图,E是四边形ABCD的边AB上一点.
(1)猜想论证:如图?,分别连接DE、CE,若∠A=∠B=∠DEC=65°,试猜想图中哪两个三角形相似,并说明理由.
(2)观察作图:如图?,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图?中矩形ABCD的边AB上画出所有满足条件的点E(点E与点A,B 不重合),分别连结ED,EC,使四边形ABCD被分成的三个三角形相似(不证明).
(3)拓展探究:如图?,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好将四边形ABCM分成的三个三角形相似,请直接写出$\frac{BC}{AB}$的值.
分析 (1)△ADE∽△BEC,理由为:利用三角形内角和定理及邻补角定义得到一对角相等,再由已知角相等,利用两角相等的三角形相似即可得证;
(2)如图②a与图②b所示,点E为所求的点;
(3)由点E恰好将四边形ABCM分成的三个三角形相似,利用相似三角形对应角相等得到三个角相等,再由折叠的性质得到∠DCM=∠MCE=∠BCE=30°,EC=CD=AB,在Rt△BCE中,利用锐角三角函数定义求出所求式子比值即可.
解答 解:(1)△ADE∽△BEC,理由为:
∵∠A=65°,
∴∠ADE+∠DEA=115°,
∵∠DEC=65°,
∴∠BEC+∠DEA=115°,
∴∠ADE=∠BEC,
∵∠A=∠B,
∴△ADE∽△BEC;
(2)作图如下:
(3)∵点E恰好将四边形ABCM分成的三个三角形相似,
∴△AEM∽△BCE∽△ECM,
∴∠BCE=∠ECM=∠AEM,
由折叠可知:△ECM≌△DCM,
∴∠ECM=∠DCM,CE=CD,
∴∠BCE=∠ECM=∠DCM=30°,
∴DC=CE=AB,
在Rt△BCE中,cos∠BCE=$\frac{BC}{EC}$=cos30°,
∴$\frac{BC}{AB}$=$\frac{\sqrt{3}}{2}$.
点评 此题属于相似型综合题,涉及的知识有:相似三角形的判定与性质,锐角三角函数定义,以及折叠的性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
5.下列有理数的大小比较,正确的是( )
| A. | -2.9>3.1 | B. | -10>-9 | C. | -4.3<-3.4 | D. | 0<-20 |
10.关于函数y=-2x+3,下列说法中不正确的是( )
| A. | 该函数是一次函数 | B. | 该函数的图象经过一、二、四象限 | ||
| C. | 当x值增大时,函数y值也增大 | D. | 当x=-1时,y=5 |
 如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线. 在△ABC中,AB=AC,∠A=36°,DE是AB的垂直平分线,DE交AB于点D,交AC于点E,连接BE.下列结论①BE平分∠ABC;②AE=BE=BC;③△BEC周长等于AC+BC;④E点是AC的中点.其中正确的结论有①②③(填序号)
在△ABC中,AB=AC,∠A=36°,DE是AB的垂直平分线,DE交AB于点D,交AC于点E,连接BE.下列结论①BE平分∠ABC;②AE=BE=BC;③△BEC周长等于AC+BC;④E点是AC的中点.其中正确的结论有①②③(填序号)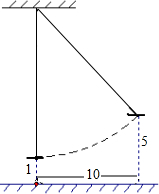 如图所示,有一架绳索拉直的秋千,当它静止时,踏板与地面的距离为1尺;将它往前推进10尺,踏板与地面的距离就为5尺.
如图所示,有一架绳索拉直的秋千,当它静止时,踏板与地面的距离为1尺;将它往前推进10尺,踏板与地面的距离就为5尺.