题目内容
20．
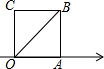正方形OABC的顶点O，A都在数轴上，点O是原点，点A对应的实数为1，对角线OB绕点O顺时针旋转45°，点B落在数轴上，此时点B所对应的实数为$\sqrt{2}$．
分析 图中正方形的边长为1，根据勾股定理求出OB的长度．由正方形的性质可知∠AOB=45°，对角线OB绕点O顺时针旋转45°，设点B落在数轴上点D的位置，则OD=OB．
解答 
解：∵四边形OABC是正方形，边长为1，
∴∠AOB=45°，OB=$\sqrt{2}$，
∵对角线OB绕点O顺时针旋转45°，设点B落在数轴上点D的位置，
∴点D在数轴的正半轴上，
∴OD=OB=$\sqrt{2}$，
∴点B所对应的实数为$\sqrt{2}$．
故答案为$\sqrt{2}$．
点评 本题考查了实数与数轴，勾股定理，正方形以及旋转的性质，比较简单．
练习册系列答案
相关题目
10．2014年十一黄金周期间，罗浮山风景区在7天假期中每天旅游的人数变化如表（正数表示比前一天多的人数，负数表示比前一天少的人数）：
（1）请判断七天内游客人数最多的是哪天？最少的是哪天？它们相差多少万人？
（2）若9月30日的游客人数为0.3万人，求这7天的游客总人数是多少万人？
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化单位：万人 | 0.16 | 0.08 | 0.04 | -0.04 | -0.08 | 0.02 | -0.12 |
（2）若9月30日的游客人数为0.3万人，求这7天的游客总人数是多少万人？
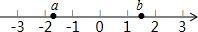实数a，b在数轴上的位置如图所示，化简：$\sqrt{（a+2）^{2}}$+$\sqrt{（b-2）^{2}}$+$\sqrt{（a-b）^{2}}$．