题目内容
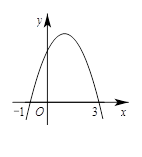
如图,四边形ABCD是矩形,A,B两点在x轴的正半轴上,C,D两点在抛物线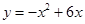 上,设OA=
上,设OA=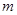 (0<
(0<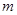 <3),矩形ABCD的周长为
<3),矩形ABCD的周长为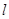 ,则
,则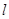 与
与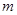 的函数解析式为
的函数解析式为 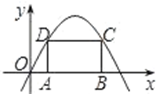
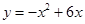 上,设OA=
上,设OA=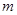 (0<
(0<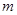 <3),矩形ABCD的周长为
<3),矩形ABCD的周长为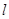 ,则
,则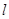 与
与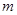 的函数解析式为
的函数解析式为 

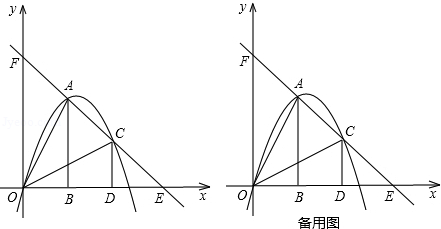
试题分析:已知C,D两点在抛物线
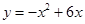 上,可知抛物线对称轴为x=
上,可知抛物线对称轴为x=
 过顶点F作FE⊥OB,垂直为E。CD所在四边形为矩形且CD在抛物线上,易知EF平分AB。所以AE=EB=OE-OA=3-m,易知D点坐标(OA,AD)则
过顶点F作FE⊥OB,垂直为E。CD所在四边形为矩形且CD在抛物线上,易知EF平分AB。所以AE=EB=OE-OA=3-m,易知D点坐标(OA,AD)则
所以矩形ABCD的周长为
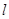 =4AE+2AD=4(3-m)+2(
=4AE+2AD=4(3-m)+2( )=
)=
点评:本题难度中等,主要考查学生对二次函数的掌握。这类题型,抓住矩形的性质确定各点坐标与抛物线的关系为解题关键,做这类题要注意数形结合思想的运用。

练习册系列答案
相关题目
 向左平移2个单位后,得到的抛物线解析式是( )
向左平移2个单位后,得到的抛物线解析式是( )



 与直线AB
与直线AB 交于x轴上的一点A,和另一点B(4,n).点P是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线PQ与直线AB垂直,交直线AB于点Q.
交于x轴上的一点A,和另一点B(4,n).点P是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线PQ与直线AB垂直,交直线AB于点Q.
 用含
用含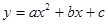 的图像交
的图像交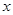 轴于
轴于 ,交
,交 轴于
轴于 ,过
,过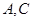 画直线。
画直线。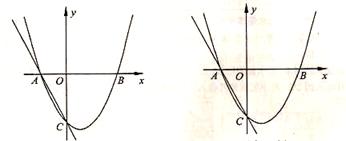
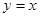 上的动点,请判断是否存在以P、Q、O、C为顶点的四边形为平行四边形,若存在,请求出点Q的坐标;若不存在,请说明理由;
上的动点,请判断是否存在以P、Q、O、C为顶点的四边形为平行四边形,若存在,请求出点Q的坐标;若不存在,请说明理由;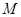 在二次函数图像上,以
在二次函数图像上,以 相切,切点为
相切,切点为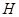 。且△CHM∽△AOC(点
。且△CHM∽△AOC(点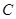 与点
与点 对应),求点
对应),求点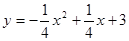 与x轴交于A、C两点,与y轴交于B点,与直线
与x轴交于A、C两点,与y轴交于B点,与直线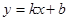 交于A、D两点。
交于A、D两点。 落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?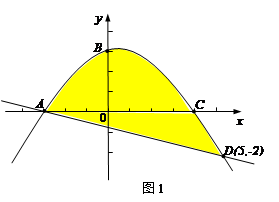
 与x轴交点是
与x轴交点是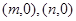 ,则
,则 的值是( )
的值是( ) 的图象如右图所示,则二次函数y=
的图象如右图所示,则二次函数y= 的图象大致为( ).
的图象大致为( ).