题目内容
9.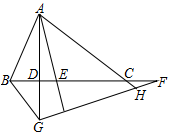 △ABC中,AD⊥BC交BC于D,AE平分∠BAC交BC于E,F为BC延长线上一点,FG⊥AE交AD的延长线于G,AC的延长线交FG于H,连接BG,下列结论:
△ABC中,AD⊥BC交BC于D,AE平分∠BAC交BC于E,F为BC延长线上一点,FG⊥AE交AD的延长线于G,AC的延长线交FG于H,连接BG,下列结论:①∠DAE=∠F;
②∠AGH=∠BAE+∠ACB;
③S△AEB:S△AEC=AB:CA;
④∠ABC+∠ACB=2∠AHG,
其中正确的结论有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 如图,①根据三角形的内角和即刻得到∠DAE=∠F;故①正确;②根据三角形的内角和和外角的性质即刻得到∠AGH=∠BAE+∠ACB;故②正确;③根据三角形角平分线定理得到$\frac{AB}{AC}=\frac{BE}{CE}$,根据三角形的面积公式即刻得到S△AEB:S△AEC=AB:CA;故③正确;④根据三角形的内角和即刻得到∠ABC+∠ACB=2∠AHG;故④正确.
解答 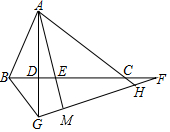 解:如图,①∵AD⊥BC,FG⊥AE,
解:如图,①∵AD⊥BC,FG⊥AE,
∴∠ADE=∠AMF=90°,
∵∠AED=∠MEF,
∴∠DAE=∠F;故①正确;
②∵∠DAE=∠F,∠FDG=∠FME=90°,
∴∠AGH=∠MEF,
∵AE平分∠BAC交BC于E,
∴∠BAE=∠CAE,
∵∠MEF=∠CAE+∠ACB,
∴∠AGH=∠CAE+∠ACB,
∴∠AGH=∠BAE+∠ACB;故②正确;
③∵AE平分∠BAC交BC于E,
∴$\frac{AB}{AC}=\frac{BE}{CE}$,
∵S△AEB:S△AEC=$\frac{\frac{1}{2}BE•AD}{\frac{1}{2}CE•AD}$=$\frac{BE}{CE}$,
∴S△AEB:S△AEC=AB:CA;故③正确;
④∵∠AMH=90°,
∴∠AHG=90°-∠CAE=90°-$\frac{1}{2}$∠BAC,
∵∠BAC=180°-∠ABC-∠ACB,
∴∠AHG=90°-$\frac{1}{2}$(180°-∠ABC-∠ACB)=$\frac{1}{2}$(∠ABC+∠ACB),
即∠ABC+∠ACB=2∠AHG;故④正确.
故选D.
点评 本题考查了角平分线的定义,三角形角平分线定理,直角三角形的性质,三角形的面积公式,正确的识别图形是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
14.9的平方根是( )
| A. | 81 | B. | 3 | C. | ±3 | D. | ±$\sqrt{3}$ |
1.任意给定一个非零数,按下列程序计算,最后输出的结果是( )


| A. | m | B. | 2m | C. | m-1 | D. | 0 |
18.如果+2%表示增加2%,那么-6%表示( )
| A. | 增加14% | B. | 增加6% | C. | 减少26% | D. | 减少6% |
19.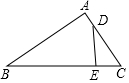 如图,在△ABC中,点D,E分别在边AC,BC上,则不一定能判断△ABC∽△EDC的是( )
如图,在△ABC中,点D,E分别在边AC,BC上,则不一定能判断△ABC∽△EDC的是( )
 如图,在△ABC中,点D,E分别在边AC,BC上,则不一定能判断△ABC∽△EDC的是( )
如图,在△ABC中,点D,E分别在边AC,BC上,则不一定能判断△ABC∽△EDC的是( )| A. | ∠CDE=∠B | B. | ∠DEC=∠A | C. | $\frac{CD}{EC}$=$\frac{CB}{AC}$ | D. | $\frac{CD}{BC}$=$\frac{DE}{BA}$ |
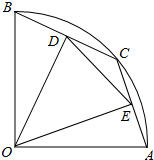 如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧$\widehat{AB}$上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧$\widehat{AB}$上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.