题目内容
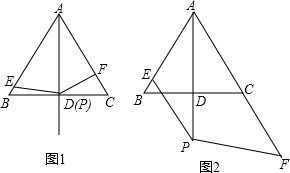
13. 如图,E为正方形ABCD的BC边上的一点,CG平分∠DCF,连接AE,并在CG上取一点G,使EG=AE,求证:AE⊥EG.
如图,E为正方形ABCD的BC边上的一点,CG平分∠DCF,连接AE,并在CG上取一点G,使EG=AE,求证:AE⊥EG.
分析 作GH⊥BF于H,先由正方形的性质可得:∠B=∠BCD=∠DCH=90°,AB=BC,然后由CG平分∠DCF,可得∠GCH=45°=∠CGH,进而可得:CH=GH,然后设CH=GH=a,BE=b,CE=c,则:AB=BC=b+c,EH=a+c,由EG=AE,可得EG2=AE2,即EH2+GH2=BE2+AB2,从而可得:(a+c)2+a2=b2+(b+c)2,进而得到:a-b=0,即a=b,所以GH=BE,然后由HL定理证明Rt△EHG≌Rt△ABE,进而得到∠HEG=∠BAE,所以∠HEG+∠BEA=∠BAE+∠BEA=90°,从而可得∠AEG=90°,即AE⊥EG得证.
解答 证明:作GH⊥BF于H.
∵四边形ABCD是正方形,
∴∠B=∠BCD=∠DCH=90°,AB=BC,
∵CG平分∠DCF,
∴∠GCH=45°=∠CGH,
∴CH=GH,
设CH=GH=a,BE=b,CE=c,则:AB=BC=b+c,EH=a+c,
∵EG=AE,
∴EG2=AE2,
即EH2+GH2=BE2+AB2,
∴(a+c)2+a2=b2+(b+c)2,
∴(a-b)(a+b+c)=0,
∵a+b+c>0,
∴a-b=0,
∴a=b,
即GH=BE,
在Rt△EHG和Rt△ABE中,
$\left\{\begin{array}{l}{AE=EG}\\{BE=GH}\end{array}\right.$,
∴Rt△EHG≌Rt△ABE(HL),
∴∠HEG=∠BAE,
∴∠HEG+∠BEA=∠BAE+∠BEA=90°,
∴∠AEG=90°,
∴AE⊥EG.
点评 此题考查了正方形的性质及全等三角形的判定与性质,解题的关键是:添加辅助线构造全等三角形.

练习册系列答案
相关题目
3.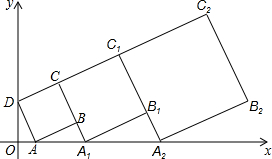 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )| A. | 5($\frac{3}{2}$)2010 | B. | 5($\frac{9}{4}$)2010 | C. | 5($\frac{9}{4}$)2011 | D. | 5($\frac{3}{2}$)2011 |
3. 通过平移后可以得到的图的是( )
通过平移后可以得到的图的是( )
 通过平移后可以得到的图的是( )
通过平移后可以得到的图的是( )| A. |  | B. |  | C. |  | D. |  |
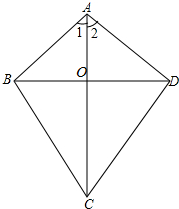 在四边形ABCD中,AC与BD相交于点D,AB=AD,BC=DC,
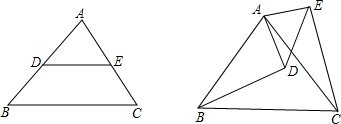
在四边形ABCD中,AC与BD相交于点D,AB=AD,BC=DC,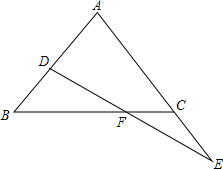 如图,在△ABC中,AB=AC,D是AB上一点,E是AC延长线上一点,且CE=BD,连结DE交BC于F.
如图,在△ABC中,AB=AC,D是AB上一点,E是AC延长线上一点,且CE=BD,连结DE交BC于F.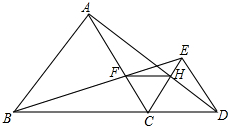 如图,已知点B,C,D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H.
如图,已知点B,C,D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H.