题目内容
17.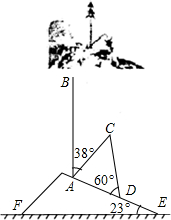 2015年4月25日14时11分尼泊尔发生了8.1级大地震.山坡上有一棵与水平面垂直的大树,大地震过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4米.
2015年4月25日14时11分尼泊尔发生了8.1级大地震.山坡上有一棵与水平面垂直的大树,大地震过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4米.(1)求∠DAC的度数;
(2)求这棵大树原来的高度是多少米?(结果精确到个位,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
分析 (1)如果延长BA交EF于点G,那么BG⊥EF,∠CAE=180°-∠BAC-∠EAG,∠BAC的度数以及确定,只要求出∠GAE即可.直角三角形GAE中∠E的度数已知,那么∠EAG的度数就能求出来了,∠CAE便可求出.
(2)在RT△ADH中,利用三角函数求得:DH=2,AH=2$\sqrt{3}$,在RT△ACH中,利用三角函数求得:AC=2$\sqrt{6}$,CH=2$\sqrt{3}$,进而求出答案.
解答 解:(1)延长BA交EF于点G.
在Rt△AGE中,∠AEG=23°,
∴∠GAE=67°.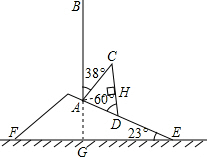
又∵∠BAC=38°,
∴∠CAD=180°-67°-38°=75°.
(2)过点A作AH⊥CD,垂足为H.
在△ADH中,∠ADC=60°,AD=4,cos∠ADC=$\frac{DH}{AD}$,
∴DH=2.
∵sin∠ADC=$\frac{AH}{AD}$,∴AH=2$\sqrt{3}$.
在Rt△ACH中,
∵∠C=180°-75°-60°=45°,CH=AH=2$\sqrt{3}$,
∴AC=2$\sqrt{6}$,CH=AH=2$\sqrt{3}$.
∴AB=AC+CD=2$\sqrt{6}$+2$\sqrt{3}$+2≈10(米).
答:这棵大树折断前高约10米.
点评 此题主要考查了解直角三角形的应用,本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
7.如图所示,∠1和∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. | 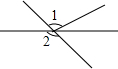 |
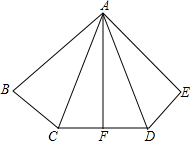 如图,已知AB=AE,∠B=∠E,BC=ED,F是CD的中点.
如图,已知AB=AE,∠B=∠E,BC=ED,F是CD的中点.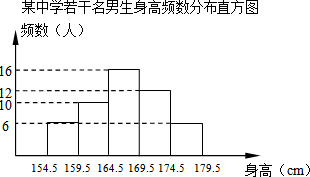 为了解某中学300名男生的身高情况,现随机抽取若干名男生进行身高测量,将所得数据整理后,画出频数分布直方图(如图),估计该校男生的身高在169.5cm~174.5cm之间的人数有72人.
为了解某中学300名男生的身高情况,现随机抽取若干名男生进行身高测量,将所得数据整理后,画出频数分布直方图(如图),估计该校男生的身高在169.5cm~174.5cm之间的人数有72人.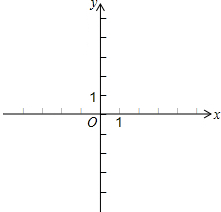 已知一次函数y1=kx+b(k≠0)的图象经过(2,0),(4,1)两点,二次函数y2=x2-2ax+4(其中a>2).
已知一次函数y1=kx+b(k≠0)的图象经过(2,0),(4,1)两点,二次函数y2=x2-2ax+4(其中a>2). 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,把图②中未被小正方形覆盖部分折成一个无盖的长方体盒子,则此长方体盒子的体积是$\frac{{a{b^2}-{b^3}}}{4}$(用a,b的代数式表示)
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,把图②中未被小正方形覆盖部分折成一个无盖的长方体盒子,则此长方体盒子的体积是$\frac{{a{b^2}-{b^3}}}{4}$(用a,b的代数式表示)