题目内容
7. 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,把图②中未被小正方形覆盖部分折成一个无盖的长方体盒子,则此长方体盒子的体积是$\frac{{a{b^2}-{b^3}}}{4}$(用a,b的代数式表示)
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,把图②中未被小正方形覆盖部分折成一个无盖的长方体盒子,则此长方体盒子的体积是$\frac{{a{b^2}-{b^3}}}{4}$(用a,b的代数式表示)
分析 直接利用图形得出长方体的长、宽、高,再利用长方体盒子体积公式进而求出即可.
解答 解:由题意知,折成的长方体盒子长、宽都为b,高为$\frac{a-b}{4}$,
故此长方体盒子的体积是:${b^2}•\frac{a-b}{4}=\frac{{a{b^2}-{b^3}}}{4}$.
故答案为:$\frac{{a{b^2}-{b^3}}}{4}$.
点评 此题主要考查了整式的混合运算,正确得出长方体的长、宽、高是解题关键.

练习册系列答案
相关题目
15.已知一个布袋里装有5个红球,3个白球,这些球除颜色外其余都相同.从该布袋里任意摸出1个球,若第一次是1个白球不放回,则第二次摸出白球的概率( )
| A. | $\frac{3}{8}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{28}$ | D. | $\frac{9}{64}$ |
12.小星同学参加体育测试的五次立定跳远的成绩(单位:米)是:1.2,1.3,1.2,1.0,1.1.这组数据的众数是( )
| A. | 1.0 | B. | 1.1 | C. | 1.2 | D. | 1.3 |
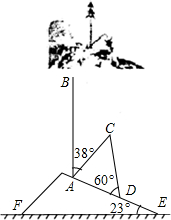 2015年4月25日14时11分尼泊尔发生了8.1级大地震.山坡上有一棵与水平面垂直的大树,大地震过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4米.
2015年4月25日14时11分尼泊尔发生了8.1级大地震.山坡上有一棵与水平面垂直的大树,大地震过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4米.