题目内容
 如同,△ABC是等边三角形,BD平分∠ABC,DE∥BC,则△ADE是什么三角形?AE与AB的大小有什么关系?为什么?
如同,△ABC是等边三角形,BD平分∠ABC,DE∥BC,则△ADE是什么三角形?AE与AB的大小有什么关系?为什么?考点:等边三角形的判定与性质,平行线的性质,等腰三角形的判定
专题:探究型
分析:根据等边三角形及平行线的性质可得到∠A=∠AED=∠ADE=60°,从而可得△AED是等边三角形,进而有AE=ED.然后由BD平分∠ABC,DE∥BC,可证到∠ABD=∠DBC=∠EDB,从而有EB=ED,即可得到AE=ED=EB,则有AE=
AB.
| 1 |
| 2 |
解答:解:△ADE是等边三角形,AE=
AB.
理由如下:∵△ABC是等边三角形,
∴∠A=∠ABC=∠ACB=60°.
∵DE∥BC,
∴∠AED=∠ABC=60°,∠ADE=∠ACB=60°,
∴∠A=∠AED=∠ADE=60°,
∴△AED是等边三角形,
∴AE=ED.
∵BD平分∠ABC,DE∥BC,
∴∠ABD=∠DBC,∠EDB=∠DBC,
∴∠ABD=∠EDB,
∴EB=ED,
∴AE=ED=EB,
∴AE=
AB.
| 1 |
| 2 |
理由如下:∵△ABC是等边三角形,
∴∠A=∠ABC=∠ACB=60°.
∵DE∥BC,
∴∠AED=∠ABC=60°,∠ADE=∠ACB=60°,

∴∠A=∠AED=∠ADE=60°,
∴△AED是等边三角形,
∴AE=ED.
∵BD平分∠ABC,DE∥BC,
∴∠ABD=∠DBC,∠EDB=∠DBC,
∴∠ABD=∠EDB,
∴EB=ED,
∴AE=ED=EB,
∴AE=
| 1 |
| 2 |
点评:本题主要考查了等边三角形的判定与性质、角平分线的定义、平行线的性质、等腰三角形的判定等知识,由本题可得到以下经验:平行线与角平分线组合常常会出现等腰三角形.

练习册系列答案
相关题目
 如图,数轴上的点P表示的实数可能是( )
如图,数轴上的点P表示的实数可能是( )A、-
| ||
B、-2
| ||
C、-
| ||
D、2
|
能清楚的看出每个项目的具体数量的统计图是( )
| A、扇形统计图 |
| B、折线统计图 |
| C、条形统计图 |
| D、以上三种均可 |
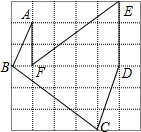 如图,这是由36个边长为1的小正方形拼成的方格图,依次连接小正方形的顶点A,B,C,D,E,F得线段AB,BC,CD,DE,EF,FA,请说出这些线段中的长度是有理数的有哪些,是无理数的有哪些,并在数轴上作出表示
如图,这是由36个边长为1的小正方形拼成的方格图,依次连接小正方形的顶点A,B,C,D,E,F得线段AB,BC,CD,DE,EF,FA,请说出这些线段中的长度是有理数的有哪些,是无理数的有哪些,并在数轴上作出表示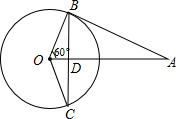 如图,AB与⊙O相切于点B,线段OA与弦BC垂直于点D,∠AOB=60°,BC=4cm,求切线AB的长.
如图,AB与⊙O相切于点B,线段OA与弦BC垂直于点D,∠AOB=60°,BC=4cm,求切线AB的长. 已知抛物线y=x2+bx+c的图象如图所示,则一元二次方程x2+bx+c=0的解是
已知抛物线y=x2+bx+c的图象如图所示,则一元二次方程x2+bx+c=0的解是 如图,在△ABC中,AF平分∠BAC,BD⊥AF,BD交AF的延长线于点D,点E在AB上,且ED∥AC,
如图,在△ABC中,AF平分∠BAC,BD⊥AF,BD交AF的延长线于点D,点E在AB上,且ED∥AC,