题目内容
 如图,△ABC中,AB=AC,CG⊥AB于G,P为BC上的一动点,PK⊥AB于K,PM⊥AC于M,探究线段PK、PM与CG之间的数量关系.
如图,△ABC中,AB=AC,CG⊥AB于G,P为BC上的一动点,PK⊥AB于K,PM⊥AC于M,探究线段PK、PM与CG之间的数量关系.考点:等腰三角形的性质
专题:
分析:连接AP,可分别表示出△ABP、△ACP和△ABC的面积,根据面积相等可找到PK、PM与CG之间的关系.
解答: 解:连接AP,
解:连接AP,
∵CG⊥AB,PK⊥AB,PM⊥AC,
∴S△ABC=
AB•CG,S△ABP=
AB•PK,S△ACP=
AC•PM,
∵S△ABC=S△ABP+S△ACP,
∴
AB•CG=
AB•PK+
AC•PM,
即AB•CG=AB•PK+AC•PM,
∵AB=AC,
∴CG=PK+PM.
 解:连接AP,
解:连接AP,∵CG⊥AB,PK⊥AB,PM⊥AC,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ABC=S△ABP+S△ACP,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即AB•CG=AB•PK+AC•PM,
∵AB=AC,
∴CG=PK+PM.
点评:本题主要考查等积法,掌握等积法的应用是解题的关键,即从不同的角度表示同一个图形的面积,从而找到相关线段之间的关系.

练习册系列答案
相关题目
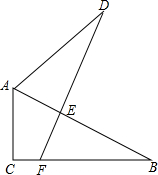 如图,Rt△ABC≌Rt△ADE中,∠C=∠AED=90°,且EF=2,BF=3,则DE=
如图,Rt△ABC≌Rt△ADE中,∠C=∠AED=90°,且EF=2,BF=3,则DE=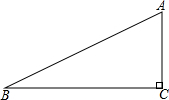 如图,Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边长,且a+b=7,c=5,求Rt△ABC的面积.
如图,Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边长,且a+b=7,c=5,求Rt△ABC的面积. 如图,△ABD≌△EBC,AB=3cm,BC=6cm,
如图,△ABD≌△EBC,AB=3cm,BC=6cm,