题目内容
15.先化简,再求值:($\frac{1}{x+1}$-$\frac{x-4}{{x}^{2}-1}$)÷$\frac{1}{x+1}$,其中x=$\sqrt{3}$+1.分析 对原式进行化简,先对括号内的式子通分,括号外面是除法可以转化为乘法,从而可将原式化简,再将x的值代入即可解答本题.
解答 解:原式=[$\frac{x-1}{(x+1)(x-1)}$-$\frac{x-4}{(x+1)(x-1)}$]÷$\frac{1}{x+1}$
=$\frac{x-1-x+4}{(x+1)(x-1)}$•(x+1)
=$\frac{3}{(x+1)(x-1)}•(x+1)$
=$\frac{3}{x-1}$.
当x=$\sqrt{3}$+1时,
原式=$\frac{3}{x-1}$=$\frac{3}{{\sqrt{3}+1-1}}$=$\frac{3}{{\sqrt{3}}}$=$\sqrt{3}$.
点评 本题考查分式的化简求值,关键是仔细认真,明确分式的加减乘除的法则即可.

练习册系列答案
相关题目
5.-1$\frac{1}{2}$的倒数是( )
| A. | -$\frac{3}{2}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
3.小明家使用的电冰箱冷藏室的温度是4℃,冷冻室比冷藏室的温度低18℃,则冷冻室的温度是( )
| A. | -14℃ | B. | 14℃ | C. | 22℃ | D. | -22℃ |
7. 如图,在△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于点E,EF∥AC,下列结论中一定成立的是( )
如图,在△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于点E,EF∥AC,下列结论中一定成立的是( )
 如图,在△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于点E,EF∥AC,下列结论中一定成立的是( )
如图,在△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于点E,EF∥AC,下列结论中一定成立的是( )| A. | ∠ABE=∠DFE | B. | AE=ED | C. | AD=DC | D. | AB=BF |
5. 如图,⊙O的半径为3,点O到直线l的距离为4,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
如图,⊙O的半径为3,点O到直线l的距离为4,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
 如图,⊙O的半径为3,点O到直线l的距离为4,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
如图,⊙O的半径为3,点O到直线l的距离为4,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )| A. | $\sqrt{7}$ | B. | $\sqrt{5}$ | C. | 4 | D. | 5 |
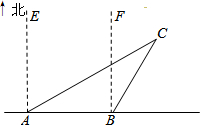 如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船的北偏东60°,40分钟后,渔船行至B处,此时看见小岛C在船的北偏东30°.
如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船的北偏东60°,40分钟后,渔船行至B处,此时看见小岛C在船的北偏东30°.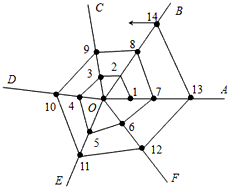 右图是蜘蛛结网过程示意图,一只蜘蛛先以O为起点结六条线OA,OB,OC,OD,OE,OF后,再从线OA上某点开始按逆时针方向依次在OA,BO,OC,OD,OE,OF,OA,OB,OF,OA,OB…上结网,若将各线上的结点依次记为1、2、3、4、5、6、7、8、…,那么第200个结点在OB条线段上.
右图是蜘蛛结网过程示意图,一只蜘蛛先以O为起点结六条线OA,OB,OC,OD,OE,OF后,再从线OA上某点开始按逆时针方向依次在OA,BO,OC,OD,OE,OF,OA,OB,OF,OA,OB…上结网,若将各线上的结点依次记为1、2、3、4、5、6、7、8、…,那么第200个结点在OB条线段上.