题目内容
3. 如图,在三角形外作正方形ABEF和ACGH,AD是BC上的高,延长DA交FH于点M.求证:FM=HM.
如图,在三角形外作正方形ABEF和ACGH,AD是BC上的高,延长DA交FH于点M.求证:FM=HM.
分析 设∠FAM=α,∠HAM=β.根据三角形的面积公式得到S△FAM=$\frac{1}{2}$AF•AM•sinα,S△HAM=$\frac{1}{2}$AH•AM•sinβ,根据正方形的性质得到∠FAB=90°,于是得到∠FAM+∠BAD=90°,由已知条件得到∠ABD+∠BAD=90°,根据余角的性质得到∠ABD=∠FAM=α,同理∠ACD=∠AHM=β,根据正弦函数的定义得到AB•sinα=AD,AC•sinβ=AD,于是推出AF•sinα=AH•sinβ,于是得到S△FAM=S△HAM.即可得到结论.
解答 证明:设∠FAM=α,∠HAM=β.
∴S△FAM=$\frac{1}{2}$AF•AM•sinα,S△HAM=$\frac{1}{2}$AH•AM•sinβ,
∵四边形ABEF是正方形,
∴∠FAB=90°,
∴∠FAM+∠BAD=90°,
∵AD⊥BC,
∴∠ABD+∠BAD=90°,
∴∠ABD=∠FAM=α,同理∠ACD=∠AHM=β,
∵AB•sinα=AD,AC•sinβ=AD.
又∵AB=AF,AC=AH,
∴AF•sinα=AH•sinβ,
∴S△FAM=S△HAM.
∴FM=HM.
点评 本题考查了正方形的性质,三角形的面积公式,垂直的定义,三角函数,熟练掌握各性质定理是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
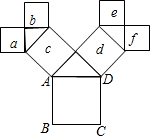 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形a,b,c,d,e,f的面积和为32,则最大的正方形ABCD的边长为4.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形a,b,c,d,e,f的面积和为32,则最大的正方形ABCD的边长为4.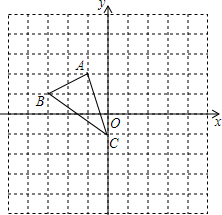 如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).
如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1). 如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有( )
如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有( )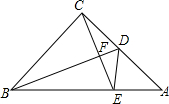 如图,从等腰Rt△ABC的直角顶点C向中线BD作垂线,交BD于点F,交AB于点E,连接DE.求证:∠CDF=∠ADE.
如图,从等腰Rt△ABC的直角顶点C向中线BD作垂线,交BD于点F,交AB于点E,连接DE.求证:∠CDF=∠ADE.