题目内容
8.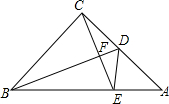 如图,从等腰Rt△ABC的直角顶点C向中线BD作垂线,交BD于点F,交AB于点E,连接DE.求证:∠CDF=∠ADE.
如图,从等腰Rt△ABC的直角顶点C向中线BD作垂线,交BD于点F,交AB于点E,连接DE.求证:∠CDF=∠ADE.
分析 在BD上截取BG=CE,利用SAS证明△ACE与△CBG全等,进而证明△ADE与△CDG全等,然后根据全等三角形的性质即可得到结论.
解答 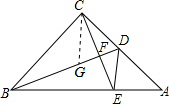 证明:在BD上截取BG=CE,连接CG,如图:
证明:在BD上截取BG=CE,连接CG,如图:
∵CE⊥BD,
∴∠BCA=∠BFC=90°,
∴∠CBF+∠BCF=∠BCF+∠ACE=90°,
∴∠CBD=∠ACE,
在△ACE与△CBG中,
$\left\{\begin{array}{l}{BC=AC}\\{∠CBD=∠ACE}\\{BG=CE}\end{array}\right.$,
∴△ACE≌△CBG(SAS),
∴CG=AE,∠BCG=∠A=45°,
∴∠GCD=45°,
在△ADE与△CDG中,
$\left\{\begin{array}{l}{CD=AD}\\{∠GCD=∠A=45°}\\{CG=AE}\end{array}\right.$,
∴△ADE≌△CDG(SAS),
∴∠CDF=∠ADE.
点评 此题考查全等三角形的判定和性质,关键是在BD上截取BG=CE,利用SAS证明△ACE与△CBG全等.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
18.在下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |

 如图,在三角形外作正方形ABEF和ACGH,AD是BC上的高,延长DA交FH于点M.求证:FM=HM.
如图,在三角形外作正方形ABEF和ACGH,AD是BC上的高,延长DA交FH于点M.求证:FM=HM. 如图,等腰三角形OBA和等腰三角形ACD的位似图形,则这两个等腰三角形位似中心的坐标是(-2,0).
如图,等腰三角形OBA和等腰三角形ACD的位似图形,则这两个等腰三角形位似中心的坐标是(-2,0).