题目内容
4. 如图,矩形的两条对角线所成的钝角为120°,若一条对角线的长是2,那么它的面积是$\sqrt{3}$.
如图,矩形的两条对角线所成的钝角为120°,若一条对角线的长是2,那么它的面积是$\sqrt{3}$.
分析 首先根据题意画出图形,然后由两条对角线相交所成的钝角为120°,证得△AOB是等边三角形,即可求得AB的长,然后由勾股定理求得BC,即可得出矩形的面积.
解答 解:在矩形ABCD中,∠AOD=120°,AC=2,
则∠AOB=60°,
∵AC=BD,OA=OC,OB=OD,
∴OA=OB=$\frac{1}{2}$AC=1,
∴△AOB是等边三角形,
∴AB=OA=1,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{3}$,
∴S矩形ABCD=BC•AB=1×$\sqrt{3}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 此题考查了矩形的性质、等边三角形的判定与性质以及勾股定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图,CD是⊙O的直径,已知∠1=30°,则∠2=( )
如图,CD是⊙O的直径,已知∠1=30°,则∠2=( )
 如图,CD是⊙O的直径,已知∠1=30°,则∠2=( )
如图,CD是⊙O的直径,已知∠1=30°,则∠2=( )| A. | 30° | B. | 45° | C. | 60° | D. | 70° |
15.下列方程变形正确的是( )
| A. | 由$\frac{1}{4}y=0$得y=4 | B. | 由3x=-5得x=-$\frac{3}{5}$ | C. | 由3-x=-2得x=3+2 | D. | 由4+x=6得x=6+4 |
16.分式方程$\frac{2x-5}{x-2}$=$\frac{3}{2-x}$的解是( )
| A. | x=-2 | B. | x=2 | C. | x=1 | D. | x=1 或 x=2 |
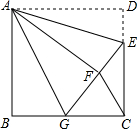 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①CE=4;②△ABG≌△AFG;③BG=GC;④AG∥CF.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①CE=4;②△ABG≌△AFG;③BG=GC;④AG∥CF.其中正确结论的个数是( ) 如图,A是反比例函数y=$\frac{k}{x}$的图象上一点,AB⊥y轴于点B,若△ABO的面积为2,则k的值为4.
如图,A是反比例函数y=$\frac{k}{x}$的图象上一点,AB⊥y轴于点B,若△ABO的面积为2,则k的值为4.