题目内容
18.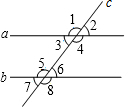 题目:如图,直线a,b被直线所截,若∠1+∠7=180°,则a∥b.在下面说理过程中的括号里填写说理依据.
题目:如图,直线a,b被直线所截,若∠1+∠7=180°,则a∥b.在下面说理过程中的括号里填写说理依据.方法一:∵∠1+∠7=180°(已知)
而∠1+∠3=180°(平角定义)
∴∠7=∠3(同角的补角相等)
∴a∥b(同位角相等,两直线平行)
方法二::∵∠1+∠7=180°(已知)
∠1+∠3=180°(平角定义)
∴∠7=∠3(同角的补角相等)
又∠7=∠6(对顶角相等)
∴∠3=∠6(等量代换)
∴a∥b(内错角相等,两直线平行)
方法三::∵∠1+∠7=180°(已知)
而∠1=∠4,∠7=∠6(对顶角相等)
∠4+∠6=180°(平角定义)
∴a∥b(同旁内角互补,两直线平行)
分析 根据平行线的判定定理进行推理论证.
解答 解:方法一:∵∠1+∠7=180°(已知)
而∠1+∠3=180°(平角定义)
∴∠7=∠3(同角的补角相等)
∴a∥b(同位角相等,两直线平行)
方法二:∵∠1+∠7=180°(已知)
∠1+∠3=180°(平角定义)
∴∠7=∠3(同角的补角相等)
又∠7=∠6(对顶角相等)
∴∠3=∠6(等量代换)
∴a∥b(内错角相等,两直线平行)
方法三:∵∠1+∠7=180°(已知)
而∠1=∠4,∠7=∠6(对顶角相等)
∠4+∠6=180°(平角定义)
∴a∥b(同旁内角互补,两直线平行).
故答案是:方法一:同角的补角相等;同位角相等,两直线平行;
方法二:同角的补角相等;对顶角相等;等量代换;内错角相等,两直线平行;
方法三:对顶角相等;同旁内角互补,两直线平行.
点评 此题考查了平行线的判定与性质,属于推理填空题,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
8. 如图,O为直线AB上一点,∠COB=26°30′,则∠1=( )
如图,O为直线AB上一点,∠COB=26°30′,则∠1=( )
 如图,O为直线AB上一点,∠COB=26°30′,则∠1=( )
如图,O为直线AB上一点,∠COB=26°30′,则∠1=( )| A. | 153°30′ | B. | 163°30′ | C. | 173°30′ | D. | 183°30′ |
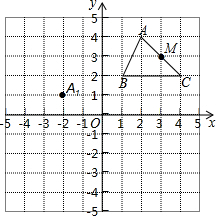 如图,在平面直角坐标系中,是边长为1的正方形网格,△ABC的顶点均在图中网格的格点上,M为AC中点.
如图,在平面直角坐标系中,是边长为1的正方形网格,△ABC的顶点均在图中网格的格点上,M为AC中点.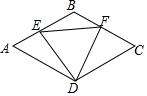 如图,在菱形ABCD中,E、F分别是AB、BC上一点,∠A=∠EDF=60°,有下列结论:①AE=BF,②△DEF 是等边三角形,③△BEF是等腰三角形,④∠ADE=∠BEF,其中正确的是( )
如图,在菱形ABCD中,E、F分别是AB、BC上一点,∠A=∠EDF=60°,有下列结论:①AE=BF,②△DEF 是等边三角形,③△BEF是等腰三角形,④∠ADE=∠BEF,其中正确的是( )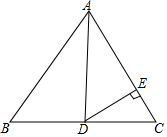 如图,在△ABC中,AD平分∠BAC,DE⊥AC,垂足为点E,∠C=48°,∠ADE=∠B,求∠B的度数.
如图,在△ABC中,AD平分∠BAC,DE⊥AC,垂足为点E,∠C=48°,∠ADE=∠B,求∠B的度数.