题目内容
3.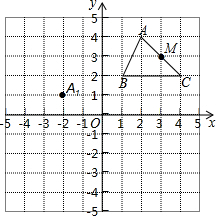 如图,在平面直角坐标系中,是边长为1的正方形网格,△ABC的顶点均在图中网格的格点上,M为AC中点.
如图,在平面直角坐标系中,是边长为1的正方形网格,△ABC的顶点均在图中网格的格点上,M为AC中点.(1)将△ABC进行平移,使得A点平移后落在A1(-2,1)处,点M的对应点M1,请你画出平移后的△A1B1C1,并直接写出B1,C1,M1的坐标;
(2)把△A1B1C1绕点M1逆时针旋转90°,得到△A2B2C2,请你画出△A2B2C2;
(3)求点B经过(1)(2)两次变换后,经过的路径长.
分析 (1)利用点A的点A1的坐标特征得到平移的规律(把△ABC先向下平移3个单位,再向左平移4个单位得到△A1B1C1),然后点平移的坐标规律写出B1,C1,M1的坐标,再描点即可得到△A1B1C1;
(2)利用网格特点和旋转的性质作出点A1、B1、C1对应点A2、B2,从而得到Rt△A2B2C2;
(3)利用勾股定理计算出平移的距离,再利用弧长公式计算出旋转过程时经过的路径长,然后把两者相加即可.
解答 解:(1)如图,△A1B1C1为所作;B1,C1,M1的坐标分别为(-3,-1),(0,-1),(-1,0);
(2)如图,△A2B2C2为所作;
(3)点B经过(1)(2)两次变换后,经过的路径长=$\sqrt{{3}^{2}+{4}^{2}}$+$\frac{90•π•\sqrt{5}}{180}$=5+$\frac{\sqrt{5}}{2}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.

练习册系列答案
相关题目
11.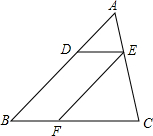 如图,点D、E、F分别在△ABC的边AB、AC、BC上,且DE∥BC,EF∥AB,若AD=$\frac{1}{2}$BD,则$\frac{{S}_{△ADE}}{{S}_{△EFC}}$=( )
如图,点D、E、F分别在△ABC的边AB、AC、BC上,且DE∥BC,EF∥AB,若AD=$\frac{1}{2}$BD,则$\frac{{S}_{△ADE}}{{S}_{△EFC}}$=( )
 如图,点D、E、F分别在△ABC的边AB、AC、BC上,且DE∥BC,EF∥AB,若AD=$\frac{1}{2}$BD,则$\frac{{S}_{△ADE}}{{S}_{△EFC}}$=( )
如图,点D、E、F分别在△ABC的边AB、AC、BC上,且DE∥BC,EF∥AB,若AD=$\frac{1}{2}$BD,则$\frac{{S}_{△ADE}}{{S}_{△EFC}}$=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
8. 如图,在△ABC中∠B=30°,∠C=90°,AD是∠CAB的平分线,DE⊥AC于点E,DE=1,则BC的长是( )
如图,在△ABC中∠B=30°,∠C=90°,AD是∠CAB的平分线,DE⊥AC于点E,DE=1,则BC的长是( )
 如图,在△ABC中∠B=30°,∠C=90°,AD是∠CAB的平分线,DE⊥AC于点E,DE=1,则BC的长是( )
如图,在△ABC中∠B=30°,∠C=90°,AD是∠CAB的平分线,DE⊥AC于点E,DE=1,则BC的长是( )| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | $\sqrt{3}+2$ |
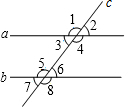 题目:如图,直线a,b被直线所截,若∠1+∠7=180°,则a∥b.在下面说理过程中的括号里填写说理依据.
题目:如图,直线a,b被直线所截,若∠1+∠7=180°,则a∥b.在下面说理过程中的括号里填写说理依据.

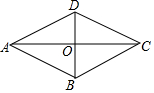 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且AC⊥BD,若AB=5 cm,DO=3cm,则△ADC的周长为18cm.
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且AC⊥BD,若AB=5 cm,DO=3cm,则△ADC的周长为18cm.