题目内容
 如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=
如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=| k |
| x |
考点:反比例函数综合题,待定系数法求反比例函数解析式,勾股定理,切线的性质,相似三角形的判定与性质
专题:压轴题
分析:设⊙P与边AB,AO分别相切于点E、D,连接PE、PD、PA,用面积法可求出⊙P的半径,然后通过三角形相似可求出CD,从而得到点P的坐标,就可求出k的值.
解答:解:设⊙P与边AB,AO分别相切于点E、D,连接PE、PD、PA,如图所示.
则有PD⊥OA,PE⊥AB.
设⊙P的半径为r,
∵AB=5,AC=1,
∴S△APB=
AB•PE=
r,S△APC=
AC•PD=
r.
∵∠AOB=90°,OA=4,AB=5,
∴OB=3.
∴S△ABC=
AC•OB=
×1×3=
.
∵S△ABC=S△APB+S△APC,
∴
=
r+
r.
∴r=
.
∴PD=
.
∵PD⊥OA,∠AOB=90°,
∴∠PDC=∠BOC=90°.
∴PD∥BO.
∴△PDC∽△BOC.
∴
=
.
∴PD•OC=CD•BO.
∴
×(4-1)=3CD.
∴CD=
.
∴OD=OC-CD=3-
=
.
∴点P的坐标为(
,
).
∵反比例函数y=
(k≠0)的图象经过圆心P,
∴k=
×
=
.
故答案为:
.
则有PD⊥OA,PE⊥AB.
设⊙P的半径为r,
∵AB=5,AC=1,
∴S△APB=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOB=90°,OA=4,AB=5,

∴OB=3.
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵S△ABC=S△APB+S△APC,
∴
| 3 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
∴r=
| 1 |
| 2 |
∴PD=
| 1 |
| 2 |
∵PD⊥OA,∠AOB=90°,
∴∠PDC=∠BOC=90°.
∴PD∥BO.
∴△PDC∽△BOC.
∴
| PD |
| BO |
| CD |
| OC |
∴PD•OC=CD•BO.
∴
| 1 |
| 2 |
∴CD=
| 1 |
| 2 |
∴OD=OC-CD=3-
| 1 |
| 2 |
| 5 |
| 2 |
∴点P的坐标为(
| 5 |
| 2 |
| 1 |
| 2 |
∵反比例函数y=
| k |
| x |
∴k=
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
故答案为:
| 5 |
| 4 |
点评:本题考查了用待定系数法求反比例函数的解析式、相似三角形的判定与性质、切线的性质、勾股定理等知识,有一定的综合性.

练习册系列答案
相关题目
下列各式:
①(-7)+(-7)=0;②(-3)2=-9;③(-2)3=-6;④-33=-27;⑤
=
.
其中运算正确的有( )
①(-7)+(-7)=0;②(-3)2=-9;③(-2)3=-6;④-33=-27;⑤
| 22 |
| 3 |
| 4 |
| 9 |
其中运算正确的有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
 若在图中三顶点以外之18个圆圈内填入适当的数,使得任何一线段上相邻三个数均成等差,则位置A所填的数为
若在图中三顶点以外之18个圆圈内填入适当的数,使得任何一线段上相邻三个数均成等差,则位置A所填的数为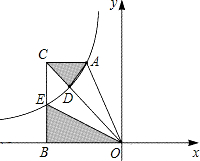 如图,在平面直角坐标系中,直角梯形AOBC的边OB在x轴的负半轴上,AC∥OB,∠OBC=90°,过A点的双曲线y=
如图,在平面直角坐标系中,直角梯形AOBC的边OB在x轴的负半轴上,AC∥OB,∠OBC=90°,过A点的双曲线y=