题目内容
如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1面积为S1,△B3D2C2面积为S2,…,△Bn+1DnCn面积为Sn,则Sn等于( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:由n+1个边长为2的等边三角形有一条边在同一直线上,则B1,B2,B3,…Bn在一条直线上,可作出直线B1B2.易求得△AB1C1的面积,然后由相似三角形的性质,易求得S1的值,同理求得S2的值,继而求得Sn的值.
解答: 解:n+1个边长为2的等边三角形有一条边在同一直线上,则B1,B2,B3,…Bn在一条直线上,作出直线B1B2.
解:n+1个边长为2的等边三角形有一条边在同一直线上,则B1,B2,B3,…Bn在一条直线上,作出直线B1B2.
∴S△AB1C1=
×2×
=
,
∵∠B1C1B2=60°,
∴AB1∥B2C1,
∴△B1C1B2是等边△,且边长=2,
∴△B1B2D1∽△C1AD1,
∴B1D1:D1C1=1:1,
∴S1=
,
同理:B2B3:AC2=1:2,
∴B2D2:D2C2=1:2,
∴S2=
,
同理:BnBn+1:ACn=1:n,
∴BnDn:DnCn=1:n,
∴Sn=
.
故选D.
 解:n+1个边长为2的等边三角形有一条边在同一直线上,则B1,B2,B3,…Bn在一条直线上,作出直线B1B2.
解:n+1个边长为2的等边三角形有一条边在同一直线上,则B1,B2,B3,…Bn在一条直线上,作出直线B1B2.∴S△AB1C1=
| 1 |
| 2 |
| 3 |
| 3 |
∵∠B1C1B2=60°,
∴AB1∥B2C1,
∴△B1C1B2是等边△,且边长=2,
∴△B1B2D1∽△C1AD1,
∴B1D1:D1C1=1:1,
∴S1=
| ||
| 2 |
同理:B2B3:AC2=1:2,
∴B2D2:D2C2=1:2,
∴S2=
2
| ||
| 3 |
同理:BnBn+1:ACn=1:n,
∴BnDn:DnCn=1:n,
∴Sn=
| ||
| n+1 |
故选D.
点评:此题考查了相似三角形的判定与性质以及等边三角形的性质.此题难度较大,属于规律性题目,注意辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
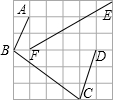 如图是由36个边长为1的小正方形拼成的,连接小正方形中的点A、B、C、D、E、F得线段AB、BC、CD、EF,这些线段中长度是有理数的是哪些?长度是无理数的是哪些?说明理由.
如图是由36个边长为1的小正方形拼成的,连接小正方形中的点A、B、C、D、E、F得线段AB、BC、CD、EF,这些线段中长度是有理数的是哪些?长度是无理数的是哪些?说明理由.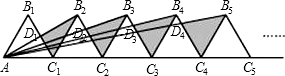

 已知△ABC,AB=3,BC=
已知△ABC,AB=3,BC=