题目内容
如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,通过计算S1,S2,…,的值,归纳出Sn的表达式(用含n的式子表示).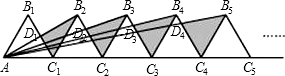
分析:由题意,等边三角形边长为2,有一条边在同一直线上,求得C1D1=1,B2到C1D1的高为
;即所求的每一个三角形的高的长度都是
;依次求C2D2的长为
,C3D3的长
,先求S1、S2、S3;归纳总结即可求得Sn的值.
| 3 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
解答:解:∵三角形为等边三角形,边长为2,
∴高为
,
∴C1D1=1;C2D2=
,C3D3=
;
∴S1=
,S2=
,
则归纳可得:Sn=
.
∴高为
| 3 |
∴C1D1=1;C2D2=
| 4 |
| 3 |
| 3 |
| 2 |
∴S1=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
则归纳可得:Sn=
| n |
| n+1 |
| 3 |
点评:此题考查了等边三角形的性质与三角形面积的求解方法.注意由一般到特殊的归纳方法,找到规律CnDn=
是解题的关键.
| n |
| n+1 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
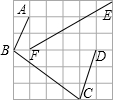 如图是由36个边长为1的小正方形拼成的,连接小正方形中的点A、B、C、D、E、F得线段AB、BC、CD、EF,这些线段中长度是有理数的是哪些?长度是无理数的是哪些?说明理由.
如图是由36个边长为1的小正方形拼成的,连接小正方形中的点A、B、C、D、E、F得线段AB、BC、CD、EF,这些线段中长度是有理数的是哪些?长度是无理数的是哪些?说明理由.
 已知△ABC,AB=3,BC=
已知△ABC,AB=3,BC=