题目内容
11.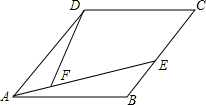 如图,四边形ABCD是菱形,点E在BC上,∠AFD=∠B,试在AE上确定一点G,使△ABG≌△DAF.请你写出两种确定点G的方案,并就其中一案的具体作法证明△ABG≌△DAF.
如图,四边形ABCD是菱形,点E在BC上,∠AFD=∠B,试在AE上确定一点G,使△ABG≌△DAF.请你写出两种确定点G的方案,并就其中一案的具体作法证明△ABG≌△DAF.方案一:作法:在AE上截取AG=DF;;
方案二:(1)作法:作∠ABG=∠DAF交AE于点G;.
(2)证明:
分析 方案一:需根据菱形的性质和全等三角形的判定即可求出点G;
方案二:(1)需根据菱形的性质和全等三角形的判定即可求出点G;
(2)根据方案一的作法再进行证明即可.
解答 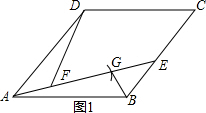 解:方案一:作法:如图1,在AE上截取AG=DF,则△ABG≌△DAF;
解:方案一:作法:如图1,在AE上截取AG=DF,则△ABG≌△DAF;
故答案为:在AE上截取AG=DF,
方案二:(1)作法:如图2,作∠ABG=∠DAF交AE于点G,则△ABG≌△DAF;
故答案为:作∠ABG=∠DAF交AE于点G;
(2)∵四边形ABCD是菱形,
∴AD∥BC,AD=AB.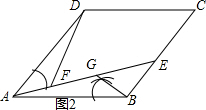
∴∠DAF=∠AEB,
∵∠AFD=∠B,
∴∠ADF=∠EAB,
由方案一的作法知:AG=DF,
在△ABG与△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ADF=∠GAB}\\{AG=DF}\end{array}\right.$,
∴△ABG≌△ADF.
点评 本题考查了菱形的性质,基本作图,全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
相关题目
1.为了参加市中学生篮球运动会,一支校篮球队准备购买10双运动鞋,各种尺码的统计如下表所示,则这10双运动鞋尺码的众数和中位数分别为( )
| 尺码/厘米 | 25 | 25.5 | 26 | 26.5 | 27 |
| 购买量/双 | 2 | 4 | 2 | 1 | 1 |
| A. | 25.5,26 | B. | 26,25.5 | C. | 26,26 | D. | 25.5,25.5 |
6.已知⊙O的半径为2,则⊙O的内接正三角形的面积为( )
| A. | $\frac{3}{2}\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
16.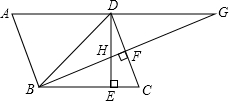 在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:
在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:
①BD=$\sqrt{2}$BE;②∠A=∠BHE;③CD2+BG2=AG2;④BH×DG=ED×GH.
正确的结论是( )
 在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:
在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:①BD=$\sqrt{2}$BE;②∠A=∠BHE;③CD2+BG2=AG2;④BH×DG=ED×GH.
正确的结论是( )
| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①②③④ |
1.据《梧州日报》报道,梧州黄埔化工药业有限公司位于万秀区松脂产业园,总投资119000000元,数字119000000用科学记数法表示为( )
| A. | 119×106 | B. | 11.9×107 | C. | 1.19×108 | D. | 0.119×109 |