Question

10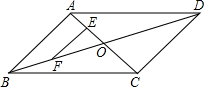．如图，平行四边形ABCD的对角线AC、BD相交于点O，点E、F分别是线段AO、BO的中点，若AC+BD=30cm，△OAB的周长为23cm，则EF的长为4cm．

Answer 1

分析 由条件AC+BD=30cm，根据平行四边形的性质可得出OA+OB=15cm，由条件△OAB的周长为23cm，可求出AB的长，再判断EF是△OAB的中位线即可得出EF的长度．

解答 解：∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
又∵AC+BD=30cm，
∴OA+OB=15cm，
∵△OAB的周长是23cm，
∴AB=8cm，
∵点E，F分别是线段AO，BO的中点，
∴EF是△OAB的中位线，
∴EF=$\frac{1}{2}$AB=4cm．
故答案为：4．

点评 本题考查了三角形的中位线定理，解答本题需要用到：平行四边形的对角线互相平分，三角形中位线的判定定理及性质．