题目内容
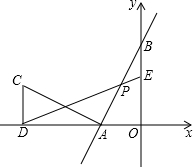 直线y=
直线y=| 5 |
| 2 |
(1)求证:AC=AB,且AC⊥AB;
(2)在y轴上取点E(0,3),连DE交AB于点P,求∠APD的度数.
考点:一次函数图象上点的坐标特征
专题:
分析:(1)根据直线解析式求出OA、OB,根据点C的坐标求出CD、OD,再求出AD,然后利用“边角边”证明△AOB和△CDA全等,根据全等三角形对应边相等可得AC=AB,全等三角形对应角相等可得∠CAD=∠ABO,再求出∠BAC=90°,然后根据垂直的定义证明即可;
(2)利用待定系数法求出直线AC、DE的解析式,设AC、DE相交于点Q,然后联立直线解析式求出点P、Q的坐标,再利用勾股定理列式求出AP2、AQ2,判断出△APQ是等腰直角三角形,再根据等腰直角三角形的性质解答.
(2)利用待定系数法求出直线AC、DE的解析式,设AC、DE相交于点Q,然后联立直线解析式求出点P、Q的坐标,再利用勾股定理列式求出AP2、AQ2,判断出△APQ是等腰直角三角形,再根据等腰直角三角形的性质解答.
解答:(1)证明:令y=0,则
x+5=0,解得x=-2,
令x+0,则y=5,
所以,OA=2,OB=5,
∵点C(-7,2),CD⊥x轴,
∴CD=2,OD=7,
∴AD=OD-OA=7-2=5,
∴OA=CD,OB=AD,
在△AOB和△CDA中,
,
∴△AOB≌△CDA(SAS),
∴AC=AB,∠CAD=∠ABO,
∵∠ABO+∠BAO=90°,
∴∠CDA+∠BAO=90°,
∴∠BAC=90°,
∴AC⊥AB;
(2)解:设直线AC的解析式为y=kx+b(k≠0),
∵A(-2,0),C(-7,2),
∴
,
解得
,
∴直线AC的解析式为y=-
x-
,
设直线DE的解析式为y=mx+n,
∵点D(-7,0),E(0,3),
∴
,
解得
,
∴直线DE的解析式为y=
x+3,
联立
,
解得
,
∴点P的坐标为(-
,
),
设AC、DE相交于点Q,
联立
,
解得
,
∴点Q(-
,
),
由勾股定理得,AP2=(-
+2)2+(
)2=(
)2+(
)2,
AQ2=(-2+
)2+(
)2=(
)2+(
)2,
∴AP2=AQ2,
又∵AC⊥AB,
∴△APQ是等腰直角三角形,
∴∠APD=45°.
| 5 |
| 2 |
令x+0,则y=5,
所以,OA=2,OB=5,
∵点C(-7,2),CD⊥x轴,
∴CD=2,OD=7,
∴AD=OD-OA=7-2=5,
∴OA=CD,OB=AD,
在△AOB和△CDA中,
|
∴△AOB≌△CDA(SAS),
∴AC=AB,∠CAD=∠ABO,
∵∠ABO+∠BAO=90°,
∴∠CDA+∠BAO=90°,
∴∠BAC=90°,
∴AC⊥AB;
(2)解:设直线AC的解析式为y=kx+b(k≠0),
∵A(-2,0),C(-7,2),
∴
|
解得
|
∴直线AC的解析式为y=-
| 2 |
| 5 |
| 4 |
| 5 |
设直线DE的解析式为y=mx+n,
∵点D(-7,0),E(0,3),
∴
|
解得
|
∴直线DE的解析式为y=
| 3 |
| 7 |

联立
|
解得
|
∴点P的坐标为(-
| 28 |
| 29 |
| 75 |
| 29 |
设AC、DE相交于点Q,
联立
|
解得
|
∴点Q(-
| 133 |
| 29 |
| 30 |
| 29 |
由勾股定理得,AP2=(-
| 28 |
| 29 |
| 75 |
| 29 |
| 30 |
| 29 |
| 75 |
| 29 |
AQ2=(-2+
| 133 |
| 29 |
| 30 |
| 29 |
| 75 |
| 29 |
| 30 |
| 29 |
∴AP2=AQ2,
又∵AC⊥AB,
∴△APQ是等腰直角三角形,
∴∠APD=45°.
点评:本题考查了一次函数图象上点的坐标特征,全等三角形的判定与性质,勾股定理,两直线相交的问题,难点在于(2)联立两直线解析式求出交点坐标并判断出等腰直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下面四个图形中,∠1与∠2相等的图形有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
在等边三角形、矩形、菱形、正方形、正五边形、正六边形中是中心对称的图形有( )个.
| A、3 | B、4 | C、5 | D、6 |
 六•一儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A、B、C是弯道MN上的三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1、S2、S3,并测得S2=6(单位:平方米).OG=GH=HI.
六•一儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A、B、C是弯道MN上的三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1、S2、S3,并测得S2=6(单位:平方米).OG=GH=HI.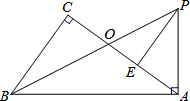 如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.
如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.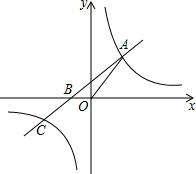 如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=(m+5)x2m+1交于点A、C,其中点A在第一象限,点C在第三象限.
如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=(m+5)x2m+1交于点A、C,其中点A在第一象限,点C在第三象限.