题目内容
13.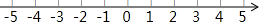 已知a,b满足(a+2)2+|b-1|=0,请回答下列问题:
已知a,b满足(a+2)2+|b-1|=0,请回答下列问题:(1)a=-2,b=1;
(2)a,b在数轴上对应的点分别为A,B,在所给的数轴上标出点A,点B;
(3)若甲、乙两个动点分别从A,B两点同时出发沿x轴正方向运动,已知甲的速度为每秒2个单位长度,乙的速度为每秒1个单位长度,请问经过多少秒甲追上乙?
分析 (1)根据非负数的性质求得a、b的值;
(2)根据(1)中的结果,在所给的数轴上标出点A,点B;
(3)设经过x秒甲追上乙,则根据路程=速度×时间和它们的运动路程相差3列出方程并解答.
解答 解:(1)∵(a+2)2+|b-1|=0,
∴(a+2)2=0,|b-1|=0,
解得 a=-2,b=1.
故答案是:-2;1;
(2)点A、B分别表示-2、1,在数轴上表示为: ;
;
(3)设经过x秒甲追上乙,则
2x=x+3,
解得 x=3.
答:经过3秒甲追上乙.
点评 本题考查了一元一次方程的应用,数轴,非负数的性质等知识点.根据非负数的性质求得点A、B所表示的数是解题的关键.

练习册系列答案
相关题目
14.下列各式的计算中,正确的是( )
| A. | a5÷a5=a5 | B. | a2•a3=a5 | C. | (a3)2=a9 | D. | a2+a3=a5 |